Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
Yu Liu*1, Suyan Tian*2, Ming-Wen An3 and Lu Wang4
Received: November 08, 2017; Published: November 15, 2017
Corresponding author:Yu Liu, Sir Run Hospital, Nanjing Medical University, 109 Longman Avenue, Nanjing, Jiangsu, China
Suyan Tian, Division of Clinical Research, First Hospital of Jilin University, 71 Xiamen Street, Changchun, Jilin, China
DOI: 10.26717/BJSTR.MS.ID.000534
Background: Crossover design is very popular for a study of new and developmental drugs. However this design tends to be misused regardless of whether it is suitable for underlying research questions.
Method: Given that in clinical practice 2x2 cross over is the most commonly used design, the Hills- Arbitrage approach is suggested to analyze data. Furthermore, we propose fitting a linear mixed model and then conducting a likelihood ratio test to yield a single p-value on data with multiple time points within each stratum.
Finding: Applying these methods to a real data, we evaluate effect of glucagon-like peptide 1 (GLP-1) on women with polycystic ovarian syndrome (PCOS). Despite absence of statistically significant results, this study as the first study to explore direct administration of GLP-1 to PCOS women is nevertheless clinically meaningful. Not only does it show a longer washout period is desired, but also it suggests GLP-1 may have the same positive effect on PCOS as MET does.
Improvement: A larger parallel study is warranted, and clinicians and biostatisticians should collaborate more so that data can be analyzed appropriately and interpreted from both statistical and clinical points of view.
Keywords: Crossover Design; Longitudinal Data; Carryover Effect; The Hills-Arbitrage Approach; Polycystic Ovarian Syndrome (Pcos)
Abbreviations: LMM: Linear Mixed Effects Model; GEE: Generalized Estimation Equations; TG: Triglyceride; TC: Total Cholesterol; HDL: High-Density Lipoprotein; LDL: Low-Density Lipoprotein; FSH: Follicle-Stimulating Hormone; E: Estradiol; T: Testosterone; LH: Luteinizing Hormone; PRL: prolactin; OGTT: Oral Glucose Tolerance Test; IQR: Inter-quantile range
In a crossover study, subjects receive a sequence of different treatments in a random order usually separated by a washout period. One major advantage of the crossover design is that the trial requires fewer patients to produce the same precision as a parallel trial, since each subject receives all treatments and thus serves as his or her own control. However, with data from crossover design trials, it is difficult to separate out treatment effects from both period and carry-over effects. Unlike a parallel clinical trial, a crossover study is typically longitudinal. However, entry- level data analysts tend to ignore the longitudinal data structure and adopt over-simplified methods intended for cross-sectional studies Mills [1] . Even when the longitudinal data structure is taken into account,period and carry-over effects are still often ignored. For example, the typical 2x2 crossover design is often mistakenly analyzed by a paired t-test Diaz-Uriarte [2,3]. Another tendency is to report the results separately for each sequence, i.e., AB and BA separately, which ultimately yields two separate estimates for the treatment effect, sometimes conflicting conclusions in which one sequence indicated treatment effect while no or hazard effect in the other.
The linear mixed effects model (LMM) and the generalized estimation equations (GEE) method are two appropriate and commonly used approaches for longitudinal data. In fact, when Zenger and Liang. Reviewed potential applications of their milestone work, GEE, they specifically used a 2x2 crossover design as an example. Unfortunately, these methods can appear computationally complicated and theoretically difficult for a clinician or an entry-level statistician. Yet in clinical practice, a 2x2 crossover design is the most commonly used design. We suggest to use the Hills-Arbitrage approach Grizzle, Hills and Arbitrage [1,4,5] to analyze data from such a design. The Hills-Arbitrage approach is essentially a two-sample t-test for a continuous variable, and is thus likely to be familiar to clinicians and entry-level statisticians. Furthermore, it had been demonstrated there were connections among LMM, GEE, and Hills-Arbitrage approach by Diaz-Uriarte [4], thus adding further appeal to the Hill-Arbitrage [1] approach. Further, we propose fitting a linear mixed model and conducting a likelihood ratio test to yield a single p-value on data from a 2x2 crossover study with multiple time points longitudinally measured within each sequence and treatment stratum. Clinicians are often concerned about whether there is a treatment effect, and thus having a single p-value on which they can make a decision is a very appealing feature. Polycystic ovarian syndrome (PCOS), a common endocrine disorder affecting 5-10% of reproductive-aged women, is a common cause of menstrual irregularity, hirsutism, and anovulatory infertility Knochenhauer, Asunción [2,6] So far, the crossover design is also a prevalent choice of evaluating the treatment effect of an intervention to PCOS, e.g., Wang [7]. It has been reported that women with PCOS may have altered in cretin hormone response Svendsen [8]. Metformin (MET) is widely used as a treatment for PCOS, probably by increasing glucagon-like peptide 1 (GLP-1) biosynthesis and secretion, thus increasing the incretion effect Svendsen [8]. This motivated us to propose direct administration of GLP-1 to women with PCOS.
Hills-Arbitrage approach: First, we give a brief describe on Hills-Arbitrage approach. Using the notation in (Diaz-Urinate 2002; Jones and Ken ward 2003), the statistical model for a 2 by 2 crossover study can be expressed as,

where πj is the period effect for the period j=1, 2, τ d is the direct treatment effect for the treatment d=A,B, Sik is the random subject effect for subject k in sequence i, and eijk is the random noise for subject k in period j and sequence I, and it is assumed that eijk ~ N (0, σ ) 2. Without loss of generality, the response variable yijk is assumed to be quantitative and to have a normal distribution. For each sequence (i.e., AB and BA), the treatment difference was calculated, yielding d12AB, namely, Y1AB -Y2AB and d21BA, namely, Y2BA-Y1BA. The Hills- Arbitrage approach tests the treatment effect (or treatment difference between A and B) by averaging the means of d12AB and d21BA. With some algebra, it can be shown that the estimator given by HA approach is unbiased for the treatment difference,τ 1- τ 2. In addition, one half of the difference between the means of d12AB and d21BA can be used as a test statistic to evaluate the period effect. Even though there is no specific parameter for the sequence effect in Equation 1, the inequality of carry-over effect in both sequences still can be tested by comparing Y1AB +Y2AB with Y1BA+Y2BA. When this is tested to be statistically significant, the Hills-Arbitrage approach suggests a two-stage procedure to evaluate on the treatment effect because the average between the means of d12AB and d21BA is subject to biases. This procedure was criticized by Freeman, Senn [6,9,10] mainly for its inflated type I error and thus potential misleading conclusions. For detailed descriptions on the Hills-Arbitrage approach, see Hills and Arbitrage, Diaz-Uriarte [1,4]. Also, interested readers are referred to Senn [9] for the diagram of the two-stage procedure of HillsArbitrage approach.
To implement the Hills-Arbitrage approach more smoothly, we may rewrite the statistical model in Equation 1 as below,
yijk = β 0 + Sik + β 1I(Period= 1)+ β 2I(sequence = AB)+β 3I(treatment = A)+ eijk (2)
Where I(x) is an indicator function and equals to one if x is true, 0 otherwise. Sik and eijk are the same as in Equation 1. In this equation, it can be easily shown that β 3 is the parameter representing treatment effect. β 1 corresponds to period effect, and β 2 corresponds to carry-over effect, providing a means to test the inequality of carry-over effects in both sequences. Using these indicators, all effects of interest are presented by a single coefficient. In a longitudinal crossover study (without loss of generality, suppose there are only 2 time points), Equation 2 may be then extended to include time points,

Where if both β 3 andβ 6 are zeros, there is no differences between A and B at either time point. The simpler model without these two parameters (the corresponding model under the alternative hypothesis) is nested within the above model (the model under the null hypothesis), thus a likelihood ratio test can be used to examine which model is a better fit. Similarly, if both β 1 and β 4 are zeros, there is no period effect. And if both β2 and β 5 are zeros, carry-over effects for both sequences are equal at either time point.
Baseline characteristics (such as age, BMI) were presented as median and Inter-quantile range (IQR). A Wilcoxon test was conducted to determine if a specific characteristic variable has the same distribution between two sequences of this crossover study. Data on those markers (e.g., GLP-1, LC) were log-transformed. A p-value < 0.05 is regarded as statistical significance. The statistical analysis was carried out in the R language version 3.1(www.r- project.org).
In this study, there were 28 PCOS accompanying with hyperinsulinemia women without use of any drugs known to alter glucose and insulin metabolism within 3 months before the study. The study was conducted in accordance with the Declaration of Helsinki and was approved by the ethics committee of Jilin University. These participants were randomized into either MET/ GLP or GLP/MET group (14 subjects in each group), and given MET (0.5g tid) and GLP-1 (5ug during the first month, then followed by 10ug for a duration of 2months) for a period of 3months. After 10 days of washout, they were crossed-over to the other treatment. Venous blood was drawn for the detection of blood lipids including triglyceride (TG), total cholesterol (TC), high-density lipoprotein (HDL), and low-density lipoprotein (LDL) using biochemical methods (Beckman, USA), the detection of 6 sex hormones including familial hyper cholesterolaemia (FH), follicle-stimulating hormone (FSH), estradiol (E2), testosterone (T), luteinizing hormone (LH), and prolactin (PRL) using radio immunoassays, the detection of fasting blood glucose levels using an oral glucose tolerance test (OGTT) with 75 g of glucose, the detection of 1-h postprandial blood glucose, and the detection of 2-h postprandial blood glucose (BIOSEN5030 blood glucose analyzer). In addition, insulin, C-peptide (electro chem. iluminescence immunoassay, Roche, Germany), active GLP-1, and total GIP levels (Enzyme-linked immuno sorbent assay, ELISA) were measured during fasting (0 min) and 15min, 30min, 60min, 120min, and 180min after glucose administration. All these measurements took place repeatedly at the baseline and at the end of each period.
Table 1: The baseline characteristics (median + IQR for continuous variables).
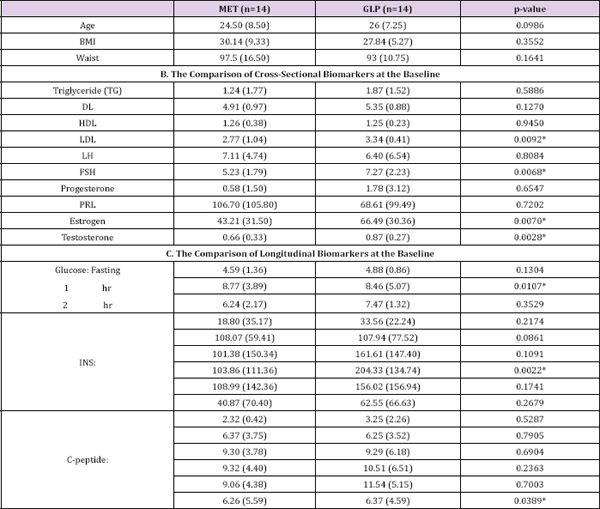
The primary objectives of this study are to compare the effects of MET vs. GLP-1 on women with PCOS accompanying with hyper insulinemia and to assess whether GLP-1 has beneficial effects on PCOS. More details of the study are provided in the Methods section. Our cross-sectional analysis on the 2x2 crossover data indicated there is no difference between GLP-1 and MET (Tables 1 & 2). However, there might exist a period effect (e.g., p=0.0039 and 0. 0029 for progesterone and PRL, respectively) and inequality of carryover between two sequences (p=0.0307 for testosterone). The washout period of 10 days was chosen based upon our preliminary studies (unpublished work) on the pharmacokinetics behaviors of GLP-1. Considering this is the first experiment testing the effect of GLP-1 on PCOS and the first test implementing crossover design, it remains unclear whether 10 days is sufficiently long to wash out the effects of GLP-1 or MET in either sequence. Our analysis suggested a longer washout period for GLP-1 might be required. (Table 3) no statistically significant difference between GLP-1 and MET on summarizes the treatment effect and period effect estimates at longitudinally measured markers, i.e., glucose, insulin (INS), and C- each time point for the longitudinal 2x2 crossover data. There is peptide.
Table 2: The comparison between GLP-1 and MET on simple endpoint.
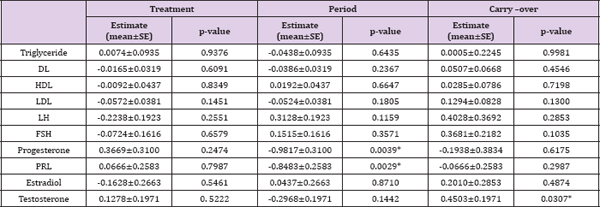
Note: The values of these markers were logarithm transformed. * p<0.05.
Table 3: The comparison between GLP-1 and MET on multiple endpoints.
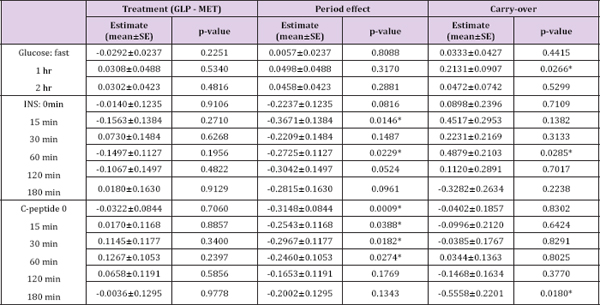
Note: The values of these markers were logarithm transformed. *p<0.05.
For the period effect testing, all p-values at all time points were bigger than 0.05 for the analysis on glucose. Based on those p-values, it may be concluded that no period effect for glucose since there exists no period effect at each time point. However, for INS and C-peptide, no definitive conclusion can be drawn because inconsistent p-values were obtained at different time points. Thus, we conducted a likelihood ratio test (see the Materials and Methods section for more details) to obtain a single p-value. P-values are 0.6921, 0.0009, and 0.0052 for INS on treatment (GLP versus MET) effect, period effect, and carry-over, respectively. P-values are 0.8181, <0.0001, and 0.0036 for treatment effect, period effect, and carry-over, respectively. It is evident that both the period effects and inequality of carryover in two sequences exist in the study. Interestingly, as shown in (Figure 1), there is an obvious pattern in the treatment difference of C-peptide and INS between GLP-1 and MET over time in spite of no statistical significance. For C-peptide, the differences reached their nadirs at the extreme time points and their peak at the middle time points (although for the GLP1- MET sequence, the peak was attained earlier than for the MET- a sharp decline followed by a gradual ascent. Further investigation GLP-1 sequence). Meanwhile, the change patterns for INS were is warranted on the biological implication beneath those patterns. approximately identical for both sequences, i.e., peak at 30 minutes, a sharp decline followed by a gradual ascent. Further investigation is warranted on the biological implication beneath those patterns.
Figure 1: Change pattern of the treatment difference between GLP-1 and MET over time.
A. C- peptide: the differences reached their nadirs at the extreme time points and their peak at the middle time points. B. INS: the change patterns for INS were approximately identical for both sequences.

The crossover design is very popular for the study of new and developmental drugs. However the crossover design tends to be adopted for its sample size savings, but without regard to whether such a design is suitable for the research question Mills [11] . Furthermore, a naïve method of analysis (e.g. paired t-test) that ignores the complexity of the design is often chosen. Another misleading preference is to obtain separate treatment effect estimates for each sequence or for each period, which sometimes yields inconsistent messages and inconclusive results. Even with consistent estimates, there is nevertheless no overall estimate of the treatment effect. Badly, these results often contribute as preliminary evidence in the literatures. Given that GEE and mixed models, two major methods used to analyze the data from a longitudinal study, are complicated for a clinician, Hills-Arbitrage approach turned out as a handy tool to deal with a crossover study. This approach is essentially a pooled t-test, and thus can be easily implemented with the aid of any statistical software. When we applied the Hills-Arbitrage approach to a PCOS data, no statistically significant results came up. First, we emphasize that GLP-1 is compared with another active agent MET, right now we only can not find evidence to support that GLP-1 is superior to MET. That cannot exclude the possibility that both GLP-1 and MET might have equal beneficial effects on PCOS in the considered markers (i.e., glucose, INS, c-peptide) herein. Also, another experiments conducted by us showed (unpublished work) that GLP-1 did improve upon some biomarkers and clinical outcomes (e.g., pregnancy).
Second, the size of this study is small even though the sample size calculation at the planning stage of this study indicated 14 per group can provide a good enough power, which was based on a large predetermined difference between the GLP-1 and MET groups. Our results may have yielded different results if we had powered the study to detect a smaller, yet still clinically significant, treatment difference. In this study, we used the raw data and have them log- transformed. Let Y1, Y2, Y3, Y4 represent period 1 baseline, period 1 outcome, period 2 baselines, and period2 outcome, respectively. Some clinicians questioned that why not use the change from the baseline instead. As demonstrated by Senn [12] that unless there is a very long washout period, the estimator using the raw data (Y2, Y4) is more efficient than that using the change from the baseline (i.e., Y2- Y1 and Y4- Y3) . Let alone there is no baseline measures (i.e., Y3) at the second period (right after the washout) in this study. If as suggested by them, the changes from the first baseline measures were evaluated (i.e., Y2-Y1and Y4-Y1 the results for treatment and period effect tests will be the same as two Y1 are cancelled out each other. For the effect of including baseline measures on carryover test, the interested readers are referred to Freeman [11] for details. However, it is always good to incorporating the baseline measures as a covariate, as suggested by Fleiss [12-16]. The results of such analysis are not shown here because of approximate same results produced. Despite the absence of statistically significant results, this study, being the first study to explore the effects of direct administration of GLP-1 to PCOS patients, is nevertheless clinically meaningful. Not only does it show a washout period longer than 10 days is desired, but also it suggests GLP-1 may have positive effect on PCOS. Certainly, a larger study using a parallel design is warranted to evaluate the treatment effects of GLP-1 on PCOS thoroughly.
This study was supported by National natural science Foundation of China (No.81170746 and No.31401123) and Norman Bethune Program of Jilin University (No. 2012214).


