A Pedagogical Description of Channel Interference in Multiphoton Absorption Processes Volume 1 - Issue 6

Mehboob Alam*

• Department of Chemistry, The Arctic University of Norway, Norway

Received: November 07, 2017;   Published: November 15, 2017

Corresponding author: Mehboob Alam, The Hylleraas Centre for Quantum Molecular Sciences, Department of Chemistry, UiT - The Arctic University of Norway, Tromsϕ, Norwa

DOI: 10.26717/BJSTR.2017.01.000532

Abstract PDF

In this mini-review, the author discusses a different view of two-photon absorption and in general any multi-photon absorption process in a molecular system in a very didactic way. This novel point of view is termed as "channel interference”. It connects the overall absorption cross section with the orientation of different transition dipole moment vectors that come into existence when a molecule undergoes two- or multiphoton absorption process. Therefore, channel interference provides an in-depth view of the process which can be used to control and fine tune the multi-photon activity in a molecular system for designing an efficient material.

Keywords: Two-photon absorption; Nonlinear optics; Response theory; Optical channels; Transition dipole moments

Abbreviations: TPA: Two-Photon Absorption; TP: Two-Photon; MPA: Multi-Photon Absorption; TDM: Transition Dipole Moment

Light-Matter Interaction

When light interacts with matter, the electric field ofthe incident light causes a distortion of the electron cloud in the molecule, which is measured in terms of polarization. A stronger electric field and loosely bound electron cloud give larger polarization than a weaker electric field and a tightly bound electron cloud. In most of the molecules, the said polarization can be expressed as a linear function of the electric field and hence the optical processes associated with this linear polarization are called linear optical processes. The normal UV-Vis or IR absorption falls into this category. Most of the molecules show this kind of absorption with UV-Vis or IR source of radiation. However, when LASER is used as incident light, polarization becomes a non-linear function of the corresponding electric field.

The optical processes associated with such non-linear polarization are called non-linear optical processes. Two-photon or multi-photon absorption and hyper-polarizabilities are the two examples of non-linear optical processes. In this mini-review, we’ll discuss the multi-photon absorption process with an emphasis on two-photon absorption (2PA) caused by a linearly polarized light.

Linear and non-linear absorptions

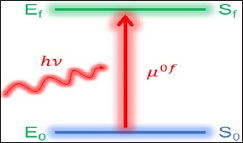
Pictorially, a linear absorption process can be shown as in Figure 1 where, S₀ and S_f represent the initial and final states respectively. E₀ and E_f are the corresponding energies of the states and hν is the energy of the incoming photon. If an incident light of low intensity is used, absorption will occur if and only if hν matches the energy gap (ω_0f = |E_f- E₀|) between the two states. If the system is centrosymmetric, then an additional requirement for an allowed transition is that the two involved states should have the different symmetry. For example, if the absorption is taking place from ground state (having gerade symmetry), in a centro-symmetric molecule, then the final excited state should have gerade symmetry [1] this is the case of linear absorption, also called one-photon absorption (1PA). This is measured in terms of oscillator strength (δ^1p) which is directly proportional to the product of «_0f and square of transition dipole moment (TDM) vector (μ^of) between initial and final states [2,3].

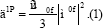
Figure 1: Pictorial representation of 1PA process.

In contrast to the linear absorption, non-linear absorptions are more complicated in mechanistic way and hence in their theoretical descriptions. A pictorial representation of first two non-linear optical absorption processes i.e. 2PA and three- photon absorption (3PA) are shown in Figure 2. MPA (M≥2) is defined as the simultaneous absorption of M-photons of same or different frequencies by a system resulting in a transition from one state to another via one or more intermediate states (S_i, S_j). The intermediate states can be either a real or a virtual state [2]. The requirement of simultaneous absorption of more than one photon is the reason why one needs a high intensity light for achieving an MPA process. In order to have an idea about the complexity of the process, let us take the case of the simplest MPA process i.e. 2PA.

Figure 2: Pictorial representation of 2PA and 3PAprocesses.

The 2PA strength of a system is measured in terms of 2PA cross section, which depends upon the following quantities - two TDM vectors μ^oi and μ^if and energy gap between the states. Additionally, δ^2p depends upon the dipole moment of the ground- and the excited-states. Thus, in 2PA the system first absorbs a photon hVj and reaches the intermediate virtual state S_i (which has a negligibly small life time), but before relaxing back to the initial state S₀, the system absorbs the second photon hv₂ and reaches the final excited state S_f. For a successful 2PA to occur, both the TDMs i.e. μ^oi and μ^if should have large values and also the time-lag between the two photons should be smaller (that means high intensity) than the life-time of the intermediate state. The 3PA and other higher order multi-photon absorption processes require more photons to be absorbed simultaneously and hence are even more complicated and even more intense light is required for observing such processes. This is the reason why we do not encounter nonlinear optical absorptions in our daily life.

For 2PA, the requirement of high values of μ^oi and μ^if indicate that the 1PA for S₀ → S_i and S_i → S_f should be allowed transitions i.e. in centrosymmetric molecules the states (S₀ and S_i) and (S_i and S_f) should have different symmetries. This requirement is fulfilled if and only if S₀ and S_f have same symmetry and S_i have symmetry different from the other two states. Thus, a 2PA process, in a centrosymmetric molecule, is allowed between states of same symmetry. The TDM vectors are also called one-photon transition moments. Similar to this, we can also define two-photon, three- photon and other multi-photon transition moments. For 2PA, the corresponding transition moment is given as [4].

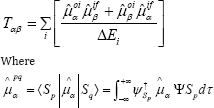
is the α^th component of TDM between p^th and q^th states and 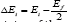The summation in Eq. 2 runs over all the electronic states of the system including ground state and αβ ϵ {X,Y, Z}. The 2PA cross section, δ^2p for single beam of a linearly polarized light is related to transition moments, T_a by the following relation [5]

Origin of Channel Interference

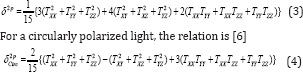
So far, we have seen that both 1PA and 2PA depends upon the magnitudes of TDM vectors between the involved states. We have also seen that in case of 1PA, only one TDM is involved whereas, in case of 2PA (as in Eq. 2) and another multi-photon absorption processes several TDMs are involved. Since TDMs are vector quantities and hence these should contribute not only through their magnitudes but also through their orientations. Thus, δ^2p should depend upon the relative orientations of different TDM involved in the process. This should also be the case for 3PA and other higher order multi-photon absorption processes. But the question is how can we separate the contributions coming from the magnitude and those coming from the relative orientations of the TDM vectors? The quantum chemistry codes like DALTON [7], GAMESS [8], TURBOMOLE [9], etc. uses quadratic response theory (details about this theory can be found somewhere else [10,11] for calculating T_αβ and δ^2p .

Because of this approach, it is not possible to get the contribution from relative orientation of the TDM vectors as neither Eq. 2 nor Eq. 3 has any orientation related term. The orientation related terms or angles between TDM vectors appear when Eq. 2 is inserted into Eq. 3 and the terms are rearranged properly. This was first done by Cronstrand, Luo and Agren [12] in 2002 for 2PA process. However, their description was limited to two-dimensional cases that means when only two components of the TDM vectors contribute. In most of the molecules, all the three components of the TDM vectors have significant contributions, which require a general three-dimensional formula. This was done, again for 2PA only by Alam, Chattopadhyaya & Chakrabarti [13] in 2012. This is called generalized few-state model (GFSM), which reads as [13].

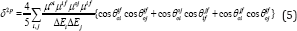
Where θ^rs_pq is the angle between two TDM vectors μ^pq and u”and other terms have their usual meanings. Eq. 5 has separated the contributions from the magnitude of the TDM vectors and those from their relative orientations. This formula, thus, can be used for studying the effect of orientation of different TDM vectors on δ^2p .

Some General Characteristics of Equation 5

It is interesting to discuss the characteristics of the generalized formula i.e. Eq. 5, because it can give important information regarding the symmetry in the process and it can also help to answer, whether such generalization is possible for other higher order MPA processes. It is interesting to note that Eq. 5 represents the overall δ^2p as a summation of interference between two channels S₀ → S_i → S_f and S₀ → S_j → S_f One can easily divide Eq. 5 into four contributions - (A) the pre-factor , (B) magnitudes of TDM vectors (numerator in the summation), (C) energy term (denominator in the summation) and (D) the orientation term (term in curly braces). Here, a brief discussion about different contributions is given.

A more comprehensive and full discussion can be found in [14]. Contribution (A) is same for all the molecules. Contribution (B) depends upon the magnitudes of a maximum of four TDMs (when i, j, and f represent different states). For a large value of , the corresponding TDMs should have large values for each state involved (i, j) in the summation. Note that, for 2PA, contribution (B) contains a maximum of four ^ terms. The third contribution i.e. (C) should have small value for a large value of δ^2p

This means, if the two incident photons have same frequency, then E_i and E. should be larger than E_f/2 i.e. the two states should lie above the mid-point between the initial and final states. Finally, contribution (D) has all cosine terms in it, each of which has a maximum value of+1. So, for a larger δ^2p, contribution (D) should be larger and close to its maximum value of +3. Note that there are altogether six cosine terms, which indicates that it includes orientation of each TDM vector relative to each of the others. The above partitioning scheme was further explored by Alam, Beerepoot and Ruud and using this, very recently, they came up with another generalization that can now be applied to any multiphoton absorption process.

Factors Affecting Channel Interference

Alam and co-workers have extensively studied [15-18] channel interference in several different kinds of molecules including both through-bond and through-space charge transfer molecules. They have shown that in general, channel interference is affected by donor-acceptor strength in the molecule, type of substitutions and their position in the molecule, polarity of the solvent, orientation of one part of the molecule relative to the other part etc. They have also studied the relative effect of donor and acceptors and concluded that donors may contribute more than acceptors [19].

Channel interference is an interesting phenomenon that can be used to fine tune the two-photon activity in a molecule. Although several factors affecting channel interference has been studied, but still these studies are limited to specific systems. The phenomenon of channel interference in different types of molecules in various different solvents can provide interesting results, which can help to provide an effective design strategy for controlling channel interference. One of the main questions still unanswered about the channel interference is that how to visualize the different transition dipole moments in a molecule. For example, the ground and excited state dipole moment can be plotted in the molecular framework but how can one plot the TDM vectors between excited states? Answer to this question may help to visualize the channel interference in a real molecular framework.

1. There are also the cases, where this symmetry requirement is relaxed. For example, if the centre of symmetry is disrupted, which can be caused by e.g. Jahn-Teller distortions, asymmetric vibrations or vibronic coupling etc. then the transition between states of same symmetry becomes allowed.
2. A virtual state is not an eigen function of the Hamiltonian of the system. It is a transient state having a very short life time. The simultaneous absorption here means that the time of absorption between the two photons is so small that the system does not get enough time to come back to the initial state from the transient/virtual state.
3. RC Hilborn (1982) Einstein coefficients cross sections, f values, dipole moments, and all that. Am J Phys 50: 982.
4. YR Shen (1984) The principles of nonlinear optics. Wiley, New York, USA, pp. 23-25.
5. WM Clain (1971) Excited State Symmetry Assignment Through Polarized Two-Photon Absorption Studies of Fluids. J Chem Phys 55: 2789.
6. K Aidas (2014) The Dalton quantum chemistry program system. WIREs Comput. Mol Sci 4(3): 269-284.
7. (2015) Dalton, a molecular electronic structure program, Release Dalton, 2016.
8. MW Schmidt, KK Baldridge, JA Boatz, ST Elbert, MS Gordon, et al. (1993) General Atomic and Molecular Electronic Structure System 14: 13471363.
9. Reinhart Ahlrichs (2016) Program Package for ab initio Electronic Structure Calculations.
10. J Olsen, P Jϕrgensen (1985) in Modern Electronic Structure Theory, (Part II, edn) Yarkony, World Scientific, Singapore, p. 857.
11. O Christiansen, C Hattig, P Jorgensen (1998) Response functions from Fourier component variational perturbation theory applied to a time- averaged quasienergy. Int J Quantum Chem 68(1): 1-52.
12. P Cronstrand, Y Luo, H 4gren (2002) Generalized few-state models for two-photon absorption of conjugated molecules. Chem Phys Lett 352: 262.
13. MM Alam, M Chattopadhyaya, S Chakrabarti (2012) Solvent induced channel interference in the two-photon absorption process-a theoretical study with a generalized few-state-model in three dimensions. Phys Chem Chem 14(3): 1156.
14. MM Alam, MTP Beerepootm, K Ruud (2017) Channel interference in multiphoton absorption. J Chem Phys 146(24): 244116.
15. MM Alam, M Chattopadhyaya, S Chakrabarti, K Ruud (2012) High-polarity solvents decreasing the two-photon transition probability of through- space charge-transfer systems-A surprising in-silico observation. J Phys Chem Lett 3(18): 961-966.
16. MM Alam (2015) Donor’s position-specific channel interference in substituted biphenyl molecules. Phys Chem Chem Phys 17(27): 1757117576.
17. MM Alam, M Chattopadhyaya, S Chakrabarti (2012) Enhancement of twist angle dependent two-photon activity through the proper alignment of ground to excited state and excited state dipole moment vectors. J Phys Chem a 116: 8067.
18. V Kunai, MM Alam, PP Thankachan (2015) Triply twisted Mobius annulene: a new class of two-photon active material - a computational study. Phys Chem Chem Phys 17(10): 6827.
19. MM Alam (2014) Donors contribute more than acceptors to increase the two-photon activity - a case study with cyclopenta [n]naphthalene based molecules. Phys Chem Phys 16(47): 26342.