info@biomedres.us
+1 (502) 904-2126
One Westbrook Corporate Center, Suite 300, Westchester, IL 60154, USA
Site Map
ISSN: 2574 -1241
ISSN: 2574 -1241
Received: August 22, 2017; Published: September 07, 2017
Corresponding author: Khoa Luu, Carnegie Mellon University, Pittsburgh, Pennsylvania, USA
DOI: 10.26717/BJSTR.2017.01.000336
Restricted Boltzmann Machines, Deep Boltzmann Machines, and their extensions have brought much attention and become powerful tools for many machine learning tasks. The increased popularity of these techniques is not only limited in modelling static data but also time-series data. In this paper, we aim to give a review of recent developments of such models for sequential data modelling. Their structures, energy functions, learning algorithm as well as applications are also provided with systematic discussions.
Keywords : Boltzmann Machines; Face Modeling; Longitudinal Face Modeling
Abbreviations: TRBM: Temporal Restricted Boltzmann Machines; RBM: Restricted Boltzmann Machines; SGD: Stochastic Gradient Descent; BB-RBM: Binary-Binary RBM; CRM: Conditional RBM; GCRBM: Gated Conditional Restricted Boltzmann Machines; TRBM: Temporal Restricted Boltzmann Machine; DBM: Deep Boltzmann Machines; AGFW: Aging Faces in the Wild; CACD: Cross-Age Celebrity Dataset
In this paper, we review the main structure of Restricted Boltzmann Machines and their improvements that have been proposed for data modeling. Different applications of this model are also summarized to provide a better understanding of the model. Notice that our work is different from the survey of recent developments of feature learning algorithms for time-series problems. The aim of that survey is to review unsupervised feature learning methods together with applications to several classical time-series problems. On the other hand, in this work, we also review recent trends and extensions of a specific model, i.e. the Temporal Restricted Boltzmann Machines (TRBM), for face modeling.
Restricted Boltzmann Machines (RBM) [1,2] are undirected graphical models consisting two layers of stochastic units, i.e. visible v and hidden units h. This is a simplified version of Boltzmann Machines where no intra connection between units in the same layer is created. RBM structure is a bipartite graph where visible and hidden units are pair wise conditionally independent. Given a binary state of {v, h}, the energy of RBM and the joint distribution of visible and hidden units can be computed as.
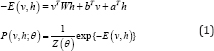
Where θ={W ,b ,a } denotes the parameter set of RBM including the connection weights; and the biases of visible and hidden units, respectively. In contrast to general BM, the inference process in RBM is exact. Thanks to this important property, the Contrastive Divergence technique can perform well to obtain the model parameters for RBM.
The conditional probabilities RBM structure can be computed as follows.
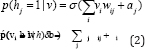
Where σ(.) is the logistic function.
In the training process of RBM, its parameters are learned to minimize the log-likelihood θ* = arg max log P(v,h;θ). The Stochastic Gradient Descent (SGD) procedure is usually employed for this optimization. The gradients are given by
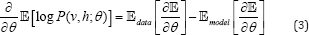
where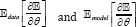 
are the Expections with respect to data distribution and distribution estimated by the RBM.
In the original RBM, both visible and hidden units are binary Therefore, it is also called as Binary-Binary RBM (BB-RBM). To make it more powerful and be able to deal with different kinds of data, RBM has received several extensions in its structures and unit types (i.e. binary, linear). This section will revise the main features of these extensions (Figure 1).
Figure 1 : Restricted Boltzmann Machines and its variants.
Gaussian Restricted Boltzmann Machines: Instead of using the binary visible units as the original RBM, Gaussian RBM [3] assumes the visible units have values in [-∞, ∞] and normally distributed with mean bi and variance σi2. By this way, this extension of RBM can be used for modelling real-valued data, i.e. pixel intensities. The energy function is modified as follows.
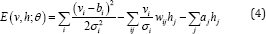
The conditional distributions over "v" and h are then given as in Eqn. (5).
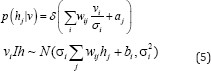
Focusing more on the RBM structure, Taylor et al. [4] introduced the Conditional RBM (CRM) to exploit the temporal relationship between consecutive frames in time-series data. Two more interactions for RBM structure, i.e. visible-to-visible and visible- to-hidden feed forward connections from previous time steps are added to the standard RBM structure. These connections are effectively incorporated to the formulation of bias terms making the learning process similar to RBM. Moreover, it can inherit most important properties of standard RBM such as simple, exact inference and efficient approximate learning. Later, Hinton [5] refined the CRBM structure by implementing the multiplicative interactions in their proposed Gated Conditional Restricted Boltzmann Machines (GCRBM). In this model, three sets of units, i.e. input, output and hidden units are first defined. Then instead of simply incorporating them via bias terms as CRBM, a three-way interaction is introduced to let the input units directly influence the interactions between units. By this way, the input units will be able to gate the basic function for reconstructing the output. The energy function is defined as
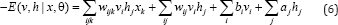
With a set of deterministic factors f, wijk can be factorized to three pair wise interactions, (1) wkfv connects to factor f; (2) wjfh connects hj to factor f; (3) wkfh connects hj to factor f.
There are several other extensions following the structure of CRBM such as factored CRBM [6] for motion style modeling; [7] with additional hierarchical structure for style interpolation; implicit Mixtures of CRBM (imCRBM) [8] that can learn from the data with several modes (e.g. walking and running in body modeling task).
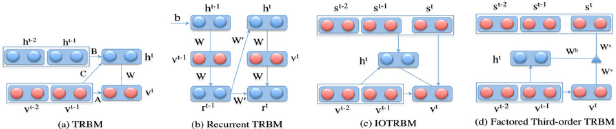
Temporal Restricted Boltzmann Machine (TRBM) [9] has gained significant attention as one of the probabilistic model that can accurately model complex time-series structure while keeping the inference tractable. The major difference between the original RBM and TRBM is the directed connections from both visible and hidden units of previous states to the current states. With these new connections, the short history of their activations can act as "memory” and is able to contribute to the inference step of current states of visible units. The joint distribution over (v‘, h‘ ) at time t is conditional on the past m states and given as
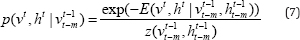
where 
are the sequence of visible and hidden units from time t-m to t-1. The energy is computed as in Eqn. (1) except the new bias terms are defined as
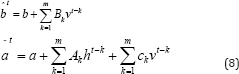
Sutskever et al. [10] later proposed the Recurrent TRBM (RTRBM) to overcome the issues of non-trivial inference step in TRBM. In RTRBM, instead of using binary hidden units, a real variable rt = 𝔼 [ht|vt is introduced and incorporated to the energy function:
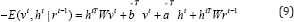
Where denotes the weights of the connections from rt-1 to ht and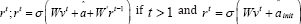 
if t=1
Other TRBM extensions consists of employing denoising Auto encoder to initialize the weights for the hidden-to-hidden connections [11]; transferring information between two sequences with Input-Output TRBM (IOTRBM) and Factor Third-order Input-Output TRBM (FIOTRBM) [12]; or removing the unnecessary connections from the fully connected topology between visible and hidden units of the RTRBM. Structured RTRBM (SRTRBM) [13]. Furthermore, in SRTRBM, the main idea is to they constructed block masking MW and MW for the weight matrices W and W model sparsely connectivity between groups of visible units and hidden units; and between groups of hidden units themselves. The authors also suggested to use spike and slab RBM instead of the GaussianRBM for better conditional covariance modeling (Figure 2).
Figure 2: Temporal Restricted Boltzmann Machines and their variants.
Deep Boltzmann Machines (DBM) [14] is a probabilistic generative model that consists of many hidden layers. Each higher layer plays a role of capturing the correlations between features of its lower layer. The structure of DBM contains several RBMs are organized in a layered manner. In DBM, the connections are between visible units and the hidden units in the first layer as well as between the hidden units in adjacent hidden layers. Thanks to this structure, the hidden units in higher layer can learned more complicated correlations of features captured in lower layer. Another interesting point of DBM is that these higher representations can be built from the training data in an unsupervised fashion. Then the labeled training data, which is assumed to be very limited, can be used to fine tune the model for a particular application. Notice that unlike other models such as Deep Belief Network [15] or Deep Auto encoders [16], all connections between units in two consecutive layers are undirected. As a result, each unit receives both bottoms- up and top-down information and, therefore, better propagate uncertainty during the inference process.
Let "v" be the set of visible units and {h(1), h(2), h(3)} be the set of units in three hidden layers, the energy of the state {v, h(1), h(2), h(3)} is given as follows.
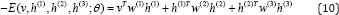
Where θ= {W (1),W (2),W(3)} are the weights of visible-to-hidden and hidden-to-hidden connections. Notice that the bias terms for visbile and hidden units are ignored in Eqn. (10) for simplifying the representation. Similar to RBM, the probability of a visible vector "v" assigned by the model is
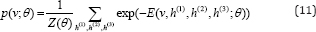
DBM is shown to be more robust with ambiguous input data [14]. Besides some recent works using DBM as shape prior model [8,17,18]. Duong et al. [19] proposed the Deep Appearance Models (DAM) for both tasks of learning high-level representation and face reconstruction under various challenging conditions. In DAM to model sparsely connectivity between groups of visible units and hidden units; and between groups of hidden units themselves. The authors also suggested to use spike and slab RBM instead of the Gaussian RBM for better conditional covariance modeling (Figure 2).structure, both shape and texture are modeled using two different DBMs. Then on the top of these two deep models, the higher-level relationships of both shape and texture are exploited so that the reconstruction of one can benefit from the information on the other. Three crucial components represented in hierarchical layers are modeled to robustly capture the variations of facial shapes and appearances. DAM is therefore superior to other classical models such as Active Appearance Models (AAM) in differencing a representation for new face images under various conditions. A robust version of DAM, named Robust Appearance Models (RDAM), is later introduced in [20] to extend its ability of dealing with occluded face regions. In the structure of RDAM, additional appearance masks is learned and help the DAM to separate corrupted/ occluded pixels in texture modeling process. As a result, those regions are ignored during face reconstruction and model fitting and, therefore, better reconstructed results can be achieved.
In addition to single face modeling, a TRBM based age progression model is introduced in [21] to embed the temporal relationship between images in a face sequence. By taking the advantages of log-likelihood objective function and avoiding the e2 reconstruction error during training, the proposed model is able to efficiently capture the non-linear aging process and automatically synthesize a series of age-progressed faces in various age ranges with more aging details. In this approach, the long-term age progresses is first decomposed into a sequence of short-term changes and model it as a face sequence. The Temporal Restricted Boltzmann Machines based age progression model together with the prototype faces are then constructed to learn the aging transformation between faces in the sequence. In addition, to enhance the wrinkles of faces in the later age ranges, the wrinkle models are further constructed using Restricted Boltzmann Machines to capture their variations in different facial regions. The geometry constraints are also taken into account in the last step for more consistent age-progressed results.
Recently, addressing a limitation of intractable learning process of TRBM based model, the Temporal Non-Volume Preserving (TNVP) approach is presented in [22] for embedding the feature transformations between faces in consecutive stages while keeping a tractable density function, exact inference and evaluation. This model shows its advantages not only in capturing the non-linear age-related variance in each stage but also producing a smooth synthesis in age progression across faces. Moreover, the structure can be transformed into a deep convolution network while keeping the advantages of probabilistic models with tractable log-likelihood density estimation. This approach is evaluated in both terms of synthesizing age-progressed faces and cross-age face verification and consistently shows the state-of-the-art results in various face aging databases, i.e. FG-NET, MORPH, our collected large-scale aging database named Aging Faces in the Wild (AGFW), and Cross-Age Celebrity Dataset (CACD).
Abstract
PDF
