ABSTRACT
The silicon capacitive pressure sensors are suitable devices for the biomedical applications due to the compatibility of the material with the human health and with the traditional technological processes of the microelectronic circuits and devices, allowing the integration with microprocessors of data in biomedical/telemedicine monitoring and low cost miniaturization. Therefore, for an accurate characterization of the micro-mechanical properties of the silicon membrane, in particular the membrane obtained from polysilicon layers, as active element of the silicon capacitive pressure sensors prepared by surface micromachining technology, it is obtained and discussed a new compact form of the theoretical relations of an electrical method applied to the beam test structures, integrated on the same micro-mechanical chip, and an accurate procedure allowing explicit analytical solutions and thus easy calculation of the Young’ modulus and residual stress, responsible for the bending of membrane, by the comparison of the theoretical calculations with the experimental data.
Keywords: Silicon Capacitive Pressure Sensors; Biomedical Applications; Electrical Test Structures; Polysilicon Beams, Accurate Procedure; Residual Stress; Young’s Modulus
Introduction
Microelectronics is nowadays a powerful contributor to our rapid development in all industrial, economics and social fields, because this became a potent tool of automation, communication, calculation, exploration, analysis and prediction [1], intervening also in biomedicine/biostatistics and healthcare [2,3], bioengineering/ biotechnology [4-7] and mass media field [8], based on the artificial intelligence and decision making [9] and unprecedented advances in the micro/nano-technologies [10,11]. Based mainly on the particular properties of silicon, a chemical element with transitory electrical conductibility between metals and isolators, and with easy processability on the entire surface areas of wafers within the planar technology, this became since the middle of the last century the central material for the fabrication of our intelligent microchips and Microelectromechanical Systems (MEMS), in particular capacitive sensors for biomedical applications [12-14]. Two main techniques are used to prepare the silicon capacitive sensors for biomedical applications: one of them based on bulk and another by surface micromachining technology, each of them allowing to obtain silicon thin membranes, with controllable micromechanical properties. Within the bulk micromachining techniques, consisting in the silicon bulk etching of preciously diffused wafers with boron high concentration to create a stop-layer of certain designed thickness [15-17], the accurate control of the thickness of the silicon layers can be obtained by the appropriate management of the diffusion [18,19] or implantation process [20], before the chemical etching. In this paper it is presented an accurate procedure for the rapid characterization of the micromechanical properties of the membrane – the key component of the of the capacitive sensors for biomedical applications, by using analytical solutions applied to an electrical method on test structures.
Silicon Capacitive Sensors and Test Method for Micromechanical Characterization
The silicon capacitive pressure sensors (SCPS) consists basically in a silicon membrane- typically circular, supported and limited by a lateral circular wall, which delimits also a cavity, where the flexible silicon membrane may bend as a function of the exercised pressure on it. Thanks to the compatibility of the silicon material with the human body and the possibility to fabricate many small units (thousands) of microstructures within the same planar technological processes, the SCPS permits a low-cost miniaturization, integrability with on-chip intelligent/ automatic data processors and versatility in novel treatments in the telemedicine, and long-term monitoring in various diseases like hypertension, hydrocephalus, or glaucoma pressure [12]. It is therefore of great importance to dispose of a rapid and accurate characterization procedure of the SCPS chips, even in earlier steps of processing, suitable for automatic measurements and evaluation on the fabrication line itself. In Figure 1 is inserted a schematic draw of a testing structure, which may be used for electrical measurements and the calculation of the residual stress (σ) and Young’s modulus (Y) of the polysilicon membrane, fabricated by surface micromachining technique.
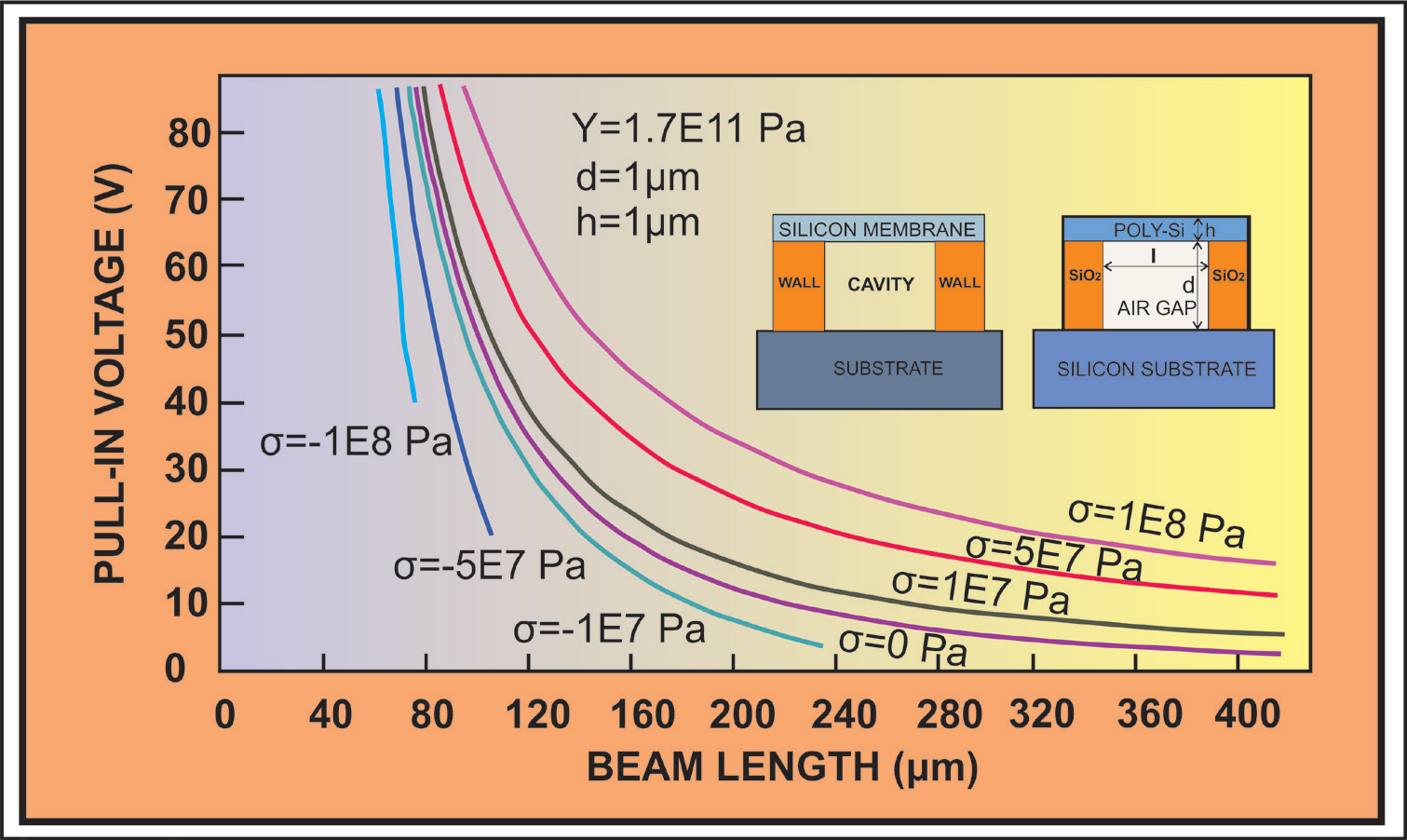
Figure 1: The variation of the beam pull-in voltage with the beam length calculated from the theoretical relations in a beam test system with d=1μm, h=1μm, Y=1.7E11 Pa and a set of positive and negative values of the residual stress in the range σ =(-1E8 Pa ÷ 1E8 Pa); in the right side are represented schematically a cross section of a silicon capacitive pressure sensor and of a test beam structure.
This technique consist in the deposition process of a polysilicon layer with a thickness h according to the designed requirements, on a silicon dioxide substrate, which is subsequently removed in an etching solution, to obtain a cavity of the high d below the membrane. The test elements are included on the same silicon wafer, and consist in at least two suspended beams with distinct lengths (l), recommendable three, with the same thickness (h) with that of the polysilicon membrane, leaving below an air gap with the height d, as it shown in the inserted draw in the right side of the Figure 1. On each of these beams is applied a voltage, which determines a flection of the beam due to the electrostatic force induced by the voltage application, till a critic position (w) followed by a sudden physical contact with the bottom electrode substrate is attained, corresponding to a critical value V of the voltage, defined as the beam pull-in voltage [21]. The conditions describing the beam pull-in voltage critic stage give rise to two equations, which can be rewritten in a new more compact form [22] as follows:
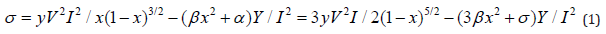
where x = w/d (w representing the critical deflection of the beam, when this is suddenly pulled down to the substrate), α=(π2 h2/3), β= (π2d2/4), γ=(εo/2π2hd3), εo representing the value of the vacuum electrical permittivity and γ = εoπ2 /16β(3αβ)½. From the last equality of the set (1) of relations, it can be deduced the following compact relation, suitable for the calculation of V if x is known, as follows:
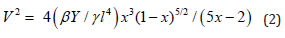
Moreover, substituting the expression γV2 l2/ x(1-x)3/2 obtained from the first equality of the set (1) of relations into the second equality of the same relation, it is obtained a new simplified equation, suitable to calculate an explicit solutions for x, as follows:
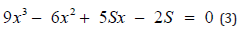
where S = (σ l2/βY + α/β). This is an equation of the third degree in x, which can be solved analytically to find an applicable real solution for S>0, and another for S<0. The real solution when S>0 is given by xo + as follows:
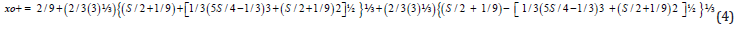
and by xo – (when S is negative), getting values into the interval [-1, 0], as follows:
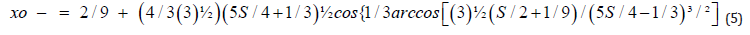
This set of relations permit the representation of the pull-in voltage V as a function of the residual stress σ and Young’s modulus Y. It is to be noted that the relation (2) expresses the dependence of V on l, as required by the experimental purpose, but also on x, a quantity which depends also on l implicitly. Therefore, it is necessary to use the real solutions of the equation (3) for S>0 and for S<0, as mentioned above, expressed by the relations (4) and (5).
Results and Discussion
In order to obtain accurate measurement data with SCPS, the values of the internal stress induced by the technological processes into the silicon membrane should be minimal, to avoid the membrane/beams deformations/bandings. A compressive residual stress is described by negative values of σ, while a tensile stress determines positive values of σ. The variation of the beam pull-in voltage with the length of the beams is represented in Figure 1 for d=1μm, h=1μm, Y=1.7E11 Pa (a typical values for polysilicon layers preciously used [21,22]) and of positive and negative values of the residual stress in the range σ =(-1E8 Pa ÷1E8 Pa); the notation E8 represents the power of 10 indicated by the exponent 8, used for the evaluation of the internal stress in the beam. In the right side are represented schematically a cross section of a silicon capacitive pressure sensor and a test beam structure. As it can be seen from this figure, the using of beams with the geometrical parameters d=1μm, h=1μm and with lengths less than about 120μm, are not recommendable for the preparation of the beam test structure, due to the very close values of pull-in voltage corresponding to small variations of the beam length, making difficult to distinguish between the curves corresponding to distinct stress values, even if they differ by an order of magnitude each other.
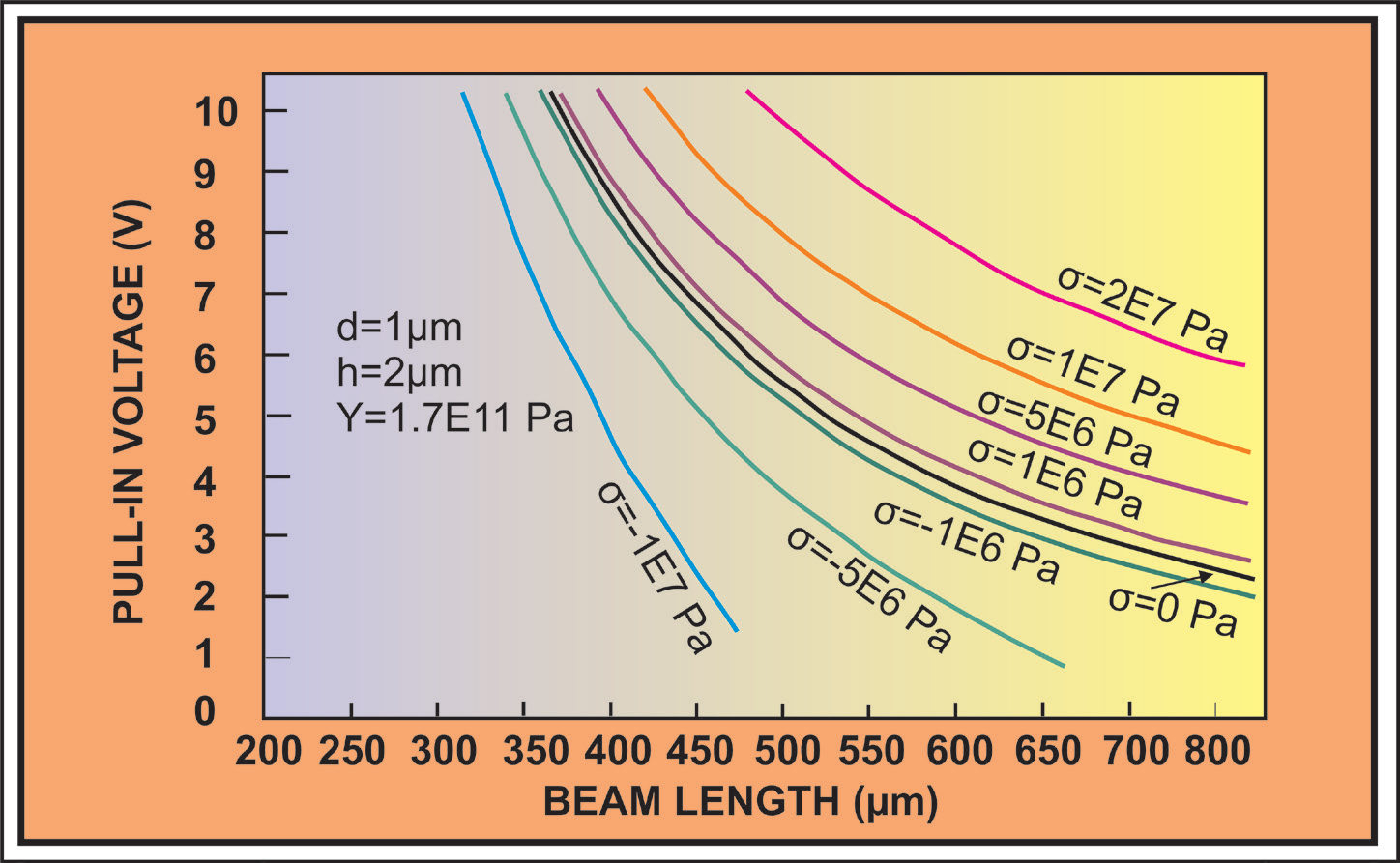
In other words, as it can be seen from Figure 1, for values of σ in the range (-1E7 Pa < σ < 1E7 Pa), small variations in the beam length produce large variations of the beam pull-in voltage, so this range is inadequate for determination of the residual stress. It can be seen also that if we refer to a beam of a length l, a compressive stress, which determines the banding of the beam, requires smaller values of the beam pull-in voltage than that for σ=0 or positive values of σ which correspond to a tensile stress in the beam, as it is also to be expected. According to the above observations, it results that in the range (-1E7 Pa < σ < 1E7 Pa), the corresponding stress induces relatively low differences between the curves V(l), showing that the residual stress in this range has low effects on the beam behavior with respect to that corresponding to σ=0 Pa. In the Figure 2, representing the variation V(l) in the range (-1E7 Pa < σ < 2E7 Pa) for a beam testing structure with h=2μm, d=1μm, Y=1.7E11 Pa, is better distinguished such a behavior.
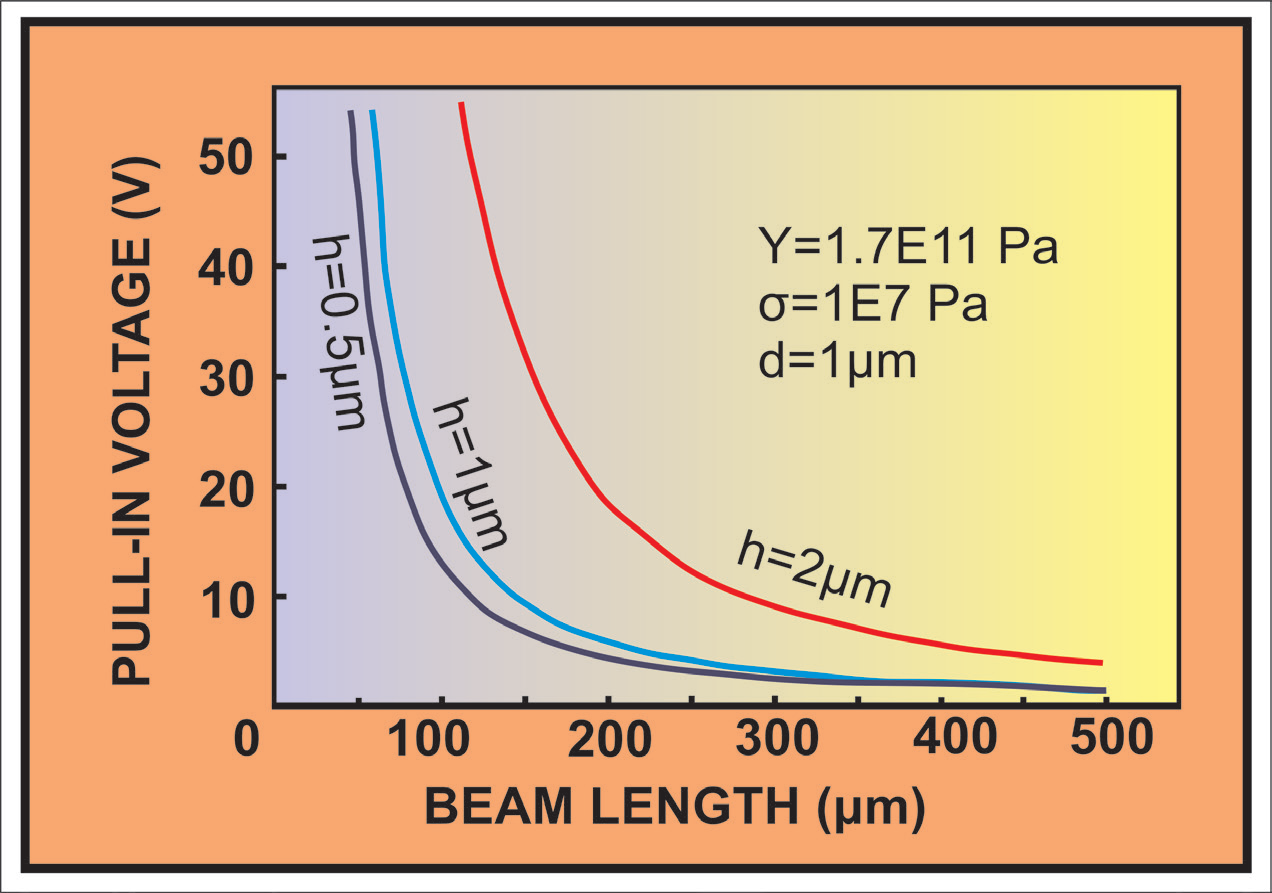
It can be observed from this figure that the variation of the value of the pull-in voltage in the interval (-1E6 Pa < σ < 2E6 Pa) is very low (less than 1V) for the same beam length, which would require a high sensitivity of the testing tool to discriminate finally the true value of σ. Such a small variation indicates actually the low effect of the residual stress on the membrane on this range. The thickness of the membrane, the same with that of the beam testing structure, is also important for the beam response. In the Figure 3 it is represented the variation of the beam pull-in voltage as a function of the beam length, for various values of the beam thickness, i.e. h=0.5 μm, h=1 μm and h=2 μm, for the same high of the air gap, d=1 μm. From this Figure results that the bending of the beam starts the later, as the greater the thickness of the beam is. The pull-in voltage values for beams with a thickness of 0.5 μm and 1 μm are close each others, for beam lengths larger than 250 μm, but very different (of the order of 10V) for the beam thickness of 2 μm.
Figure 2: Variation V(l) for V< 10 V on a test polysilicon beam structure with h=2μm, d=1μm, Y=1.7E11 Pa, for various values of the residual stress in the interval (-1E7 Pa < σ < 2E7 Pa).
Figure 3: Comparison between the variation V(l) calculated for σ=1x1E7 Pa, Y=1.7x1E11 Pa and d=1μm, corresponding to various thickness values h=2μm, 1μm and 0.5 μm of the testing beams.
These results indicate the necessity to properly design the dimensions of the beams, according to the calculations presented and discussed here, for an accurate evaluation of the mechanical properties of the beams, so of the polysilicon membrane of SCPS. For an accurate extraction of the mechanical parameters of polysilicon layers, σ and Y, the pull-in voltage method should be applied at two distinct polysilicon beams, with distinct lengths, and the mathematical relations (2) and (3), together with (4) or (5) are to be applied. A better procedure would consist in the fitting of a theoretical curve like that shown in the Figures 1-3, on three or more measurements V-l data. The comparison of the experimental data with the theoretical calculations best fitting the data, allows an accurate calculation both of the residual stress and Young’s modulus corresponding to the polysilicon layer for the preparation of the SCPSs. The accessibility of the test structures immediately after technological processes, permits the optimization of the technological process, especially the polysilicon deposition, doping and annealing treatment [23].
Conclusion
The silicon capacitive pressure sensors are very suitable devices for biomedical applications both as material and the low-cost miniaturization, the adaptability for microelectronic integration with on-chip intelligent/automatic processors of data and versatility in the novel procedures of telemedicine and monitoring in hypertension, hydrocephalus, or glaucoma pressure. In particular, the surface micromachining technology offers the possibility to use the traditional technological processes of the fabrication of the microelectronic circuits and devices and the experience accumulated on this field, and integration of the beam test structures for the measurement of the micromechanical properties of the membranes of the silicon capacitive pressure structures, specifically the residual stress and the Young’s modulus, with major effects on the final device performances. The new compact form of the relations describing the beam pull-in voltage method, leading to an equation of the third degree and explicit analytical solutions, allows an accurate and rapid preliminary calculation of the material parameters on the fabrication line for the process optimization, and appropriate design and preparation both of the silicon capacitive pressure structures and polysilicon beam tests.
Conflict of Interest
No financial interest or conflict of interest do exist.
Acknowledgment
To Professor Dr. Dimitris Tsoukalas, Professor Dr. Jaume Esteve and Professor Dr. Ryszard Jachowicz, for our close collaboration. To Adrian Gaiseanu and Ana-Maria Gaiseanu. With grateful thanks to this Journal for the kind invitation and professional publication. In the memory of my loved parents and brother, Professors Emanoil, Florica and Constantin Gaiseanu.
References
- Filip Florin Gheorghe (2020) DSS-A class of evolving information systems. In: G Dzemyda, J Bernatavičienė and J Kacprzyk (Eds.)., Data science: new issue, challenges and applications, pp. 253-277.
- Gaiseanu Florin (2021) Information in Biological Structures and Big Data Assisted Prediction as Informational Biostatistics/Biometric Tool for Pandemic COVID-19 Investigation. Annals of Biostatistics & Biometric Applications 4(3): 1-3.
- Gaiseanu Florin (2022) Virus-Inducing Informational Processes vs. Cell Antivirus Info-Sensitivity and Implication of the Biostatistics/Metric Applications in the Detection/Prediction of the Covid-19 Infections. Annals of Biostatistics & Biometric Applications 4(3): 1-5.
- Gaiseanu Florin (2021) Human as an Informational Device. Archives in Biomedical Engineering & Biotechnology 6(1): 1-8.
- Gaiseanu Florin (2021) New Perspectives in Biomedical Engineering and Biotechnology: Information in Human and Biological Structures. Archives in Biomedical Engineering and Biotechnology 6(1): 1-3.
- Gaiseanu Florin (2021) Advanced Perspectives in Biological Researches: Info-Operability of the Cell and Human/Multicellular Organisms. Acta Scientific Biotechnology 2(7): 1-5.
- Gaiseanu Florin (2022) Information as a Coherent/Effective Investigation Concept/Strategy to Approach the Biotechnology Scientific and Technical Research. Acta Scientifica Biotechnology 3(1): 28-33.
- Gaiseanu Florin (2022) The Cognitive-Sentient Exploration of Mediated Reality: From Proto-Cognition/Epigenetic Informational Processes to Big Data Assisted Prediction, Chapter in “Global Media’s Preternatural Influence on Global Technological Singularity, Culture, and Government”. In: Stephen Brock Shafer and Alex Bennet (Eds.)., IGI-Global (USA).
- Florin Gheorghe Filip (2022) Collaborative Decision-Making: Concepts and Supporting Information and Communication Technology Tools and Systems. International Journal of Computers, Communications & Control 17(2): 1-10.
- Gaiseanu Florin (2013) Contributions to the Modeling and Simulation of the Atomic Transport Processes in Silicon and Polysilicon and Applications. Proceedings of the Romanian Academy Series A, The Publishing House of the Romanian Academy 4(4): 376-384.
- Gaiseanu Florin (2017) Modelling and Simulation of the Impurity Diffusion and Related Phenomena in Silicon and Polysilicon Systems in Microfabrication and Micromachining Technologies. Annals of the Academy of Romanian Scientists Series on Science and Technology of Information 10(1): 41-78.
- Hoc Khiem (2011) Surface Micromachined Pressure Sensors for Medical Applications, D6.1 Sensor and Test Conference, pp. 618-623.
- Yongzhao Xu, Xiduo Hu, Saudi Kundu, Anindya Nag, Nasrin Afsarimanesh, et al. (2019) Silicon-Based Sensors for Biomedical Applications: A Review. Sensors 19(2908): 1-22.
- Eswaran P, Malarvizhi S (2013) MEMS Capacitive Pressure Sensors: A Review on Recent Development and Prospective. International Journal of Engineering and Technology (IJET) 3(5): 2736-2746.
- Gaiseanu F, Tsoukalas D, Goustouridis D, Esteve J, Tsoi E, et al. (1997) Analytical Modeling of the Self-Limitation Process During the Chemical Etching of Boron-Doped Silicon. Proceeding of the 11th European Conference on Solid-State Transducers (EUROSENSORS XI). In: Prof. R. Jachowicz Warsaw (Edt.)., Sept. 21-24 (3P2-9): 1283-1286.
- Gaiseanu F, Tsoukalas D, Esteve J, Postolache C, Goustouridis D, et al. (1997) Chemical Etching Control During the Self-Limitation Process by Boron Diffusion in Silicon: Analytical Results. Proc. of the International Semiconductor Conference (CAS 97), Oct. 8-11th, Sinaia, Romania, pp. 247- 250.
- Gaiseanu Florin, Esteve Jaume, Kissinger Gudrun, Kruger Dietmar (1998) Diffusion Induced Dislocations in Highly Boron-Doped Silicon Layers Used for Micromachining Applications. Symposium on Micromachining and Microfabrication organized by SPIE (The International Society for Optical Engineering - SPIE) in Santa Clara, California, Sept. 20-22, SPIE Proceeding 3511.
- Gaiseanu Florin (2022) Technology for the Accurate Preparation of Silicon Capacitive Pressure Sensors with Biomedical Application. Biomedical Journal of Scientific & Technical Research 42(4): 33790-33796.
- Gaiseanu Florin (1984) Simulation of the Boron Diffusion in Silicon from a BBr3 Source J. Meeting of ECS, Extended Abstracts (Electrochemical Society, Pennington, NJ, 1984) 84-2: 715 and Electrochem. Soc., 1131, 318C.
- Gaiseanu F, Cobianu C, Dascalu D (1993) Dependence of the Chemical Etching Rate and Etching Time on the Post-Implanted Diffusion Depth: Application for Membrane Achievement. Journal of the Material Science Letters 12: 1652 -1653.
- Quanbo Zou, Zhijian Li, Litian Liu (1995) New methods for measuring mechanical properties of thin films in micromachining: Beam pull-in voltage (VPI) method and long beam deflection (LBD) method. Sensors and Actuators A 48:137-143.
- Gaiseanu Florin (2019) Analytical Simulation of the Pull-in Voltage to Evaluate the Process Induced Stress and Ypung's Module into the Micromachining Polysilicon Layers by the Pull-in Voltage Method. Annals of the Academy of Romanian Scientists Series on Science and Technology and Information 12(1): 33-44.
- Gaiseanu F, Kruger D, Dimitriadis CA, Stoemenos J, Postolache C, et al. (1997) Influence of the Restructuring Process on the Phosphorus Doping Near the Polysilicon/SiO2 Interface on Silicon, Proc. of the International Semiconductor Conference (CAS 97) 8-11th, Sinaia, Romania, p. 67-70.

 Research Article
Research Article