ABSTRACT
The analysis of dependence of the length projection of Li vectors of biparametrical
inhibited and activated (La) enzymatic reactions from the length projection of vectors
of monoparametrical inhibited and activated enzymatic reactions on the basic 0 σ plane
in three-dimensional 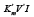 coordinate system, allows to deduct the quadratic forms of equations for the calculation of the constants of inhibition (Ki) and activation (Ka) of
enzymes. Examples of calculation of constants are given.
coordinate system, allows to deduct the quadratic forms of equations for the calculation of the constants of inhibition (Ki) and activation (Ka) of
enzymes. Examples of calculation of constants are given.
Introduction
In previous articles [1-9], devoted to construction of a vector
method representation of enzymatic reactions in the threedimensional 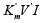 coordinate system the properties of L vectors
of enzymatic reactions was analyzed, from which the parametriacal
classification of the types of enzymatic reactions and the equations
for calculation of initial activated (Va ) and inhibited (Vi ) reaction
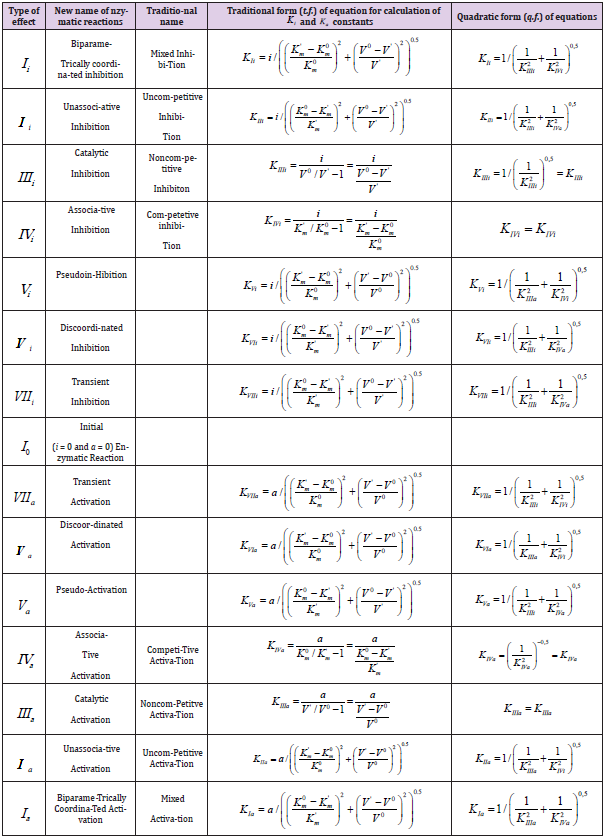
rates was suggested. In these article the equations of traditional
form (t.f.) for calculation of the constants of activation (Ka) and
absent in practice nontrivial types of biparametrical constants of
inhibition (Ki) of enzymes (Table 1), was deduced.
coordinate system the properties of L vectors
of enzymatic reactions was analyzed, from which the parametriacal
classification of the types of enzymatic reactions and the equations
for calculation of initial activated (Va ) and inhibited (Vi ) reaction
rates was suggested. In these article the equations of traditional
form (t.f.) for calculation of the constants of activation (Ka) and
absent in practice nontrivial types of biparametrical constants of
inhibition (Ki) of enzymes (Table 1), was deduced.
This work is devoted to deduction of quadratic form (q.f.) of the
equations for calculation of biparametrical constants of inhibition
and activation of enzymes (Table 1t & 1f), opening additional ability
in the analysis of enzyme action what help of quadratic forms of
equation (Table 1q& 1f).
The examples of comparative using traditional and quadratic
form of equations for calculation of Ki and Ka constants of inhibition
and activation are given.
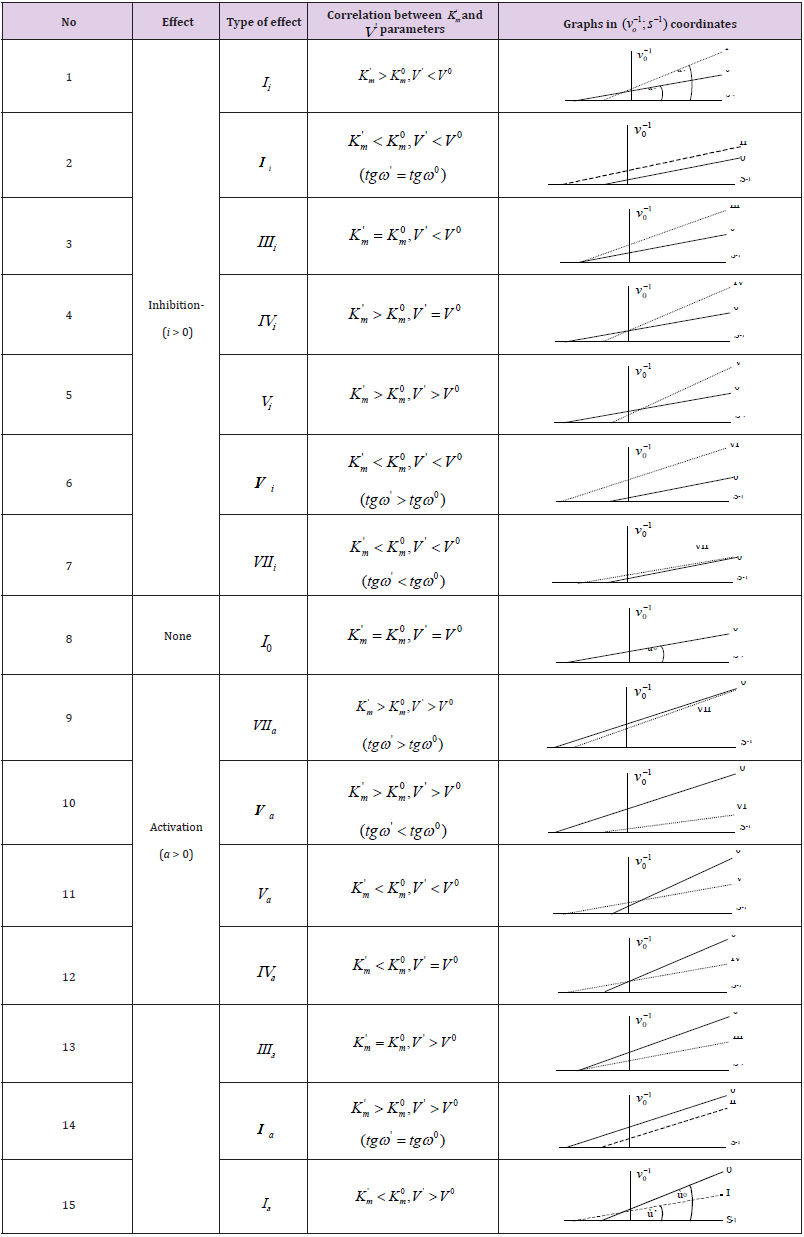
Table 1: Equations for calculation of Ki and Ka constants (in traditional form).
*The symbol of a graph in Figs. 1-15 corresponds to the type of reaction under study. For example: the line (0) characterizes the position of initial (nonactivated) enzymatic reaction, line I – the position of a graph representing the type of activated enzymatic reaction etc.
Deduction of Traditional form of Equations
From (Figures 1, 1a and 2) it easy to see, that ( Ii l ) length of
(LIi) projection of LIi vector of biparametrically coordinated, i I
type (or mixed type [10 -12]) of enzyme inhibition on Pi semiaxis
will be determined by divide (i-0) parameters on ( Ii l ) length of
(LIi) projection of LIi vector of – by summation of the quadratic (l2)
lengths (orthogonal between them self) LIIIi and LIVi projections of
monoparametrical LIIIi and LIVi vectors of i III and 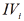 type of enzyme
inhibition, (which also are the coordinate of these vectors) but in
the same time they taking adjacent place relative to orthogonal LIi
projection of LIi vector (Figure 2), determined by equation:
type of enzyme
inhibition, (which also are the coordinate of these vectors) but in
the same time they taking adjacent place relative to orthogonal LIi
projection of LIi vector (Figure 2), determined by equation:
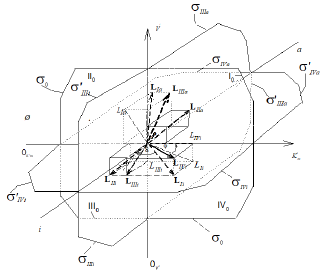
Figure 1: Three dimensional (incompletely) system of rectangular coordinate with separately Pi and Pa semiaxes of molar concentrations of [i] inhibitor and [a] activator. Only 8 L vectors of enzymatic reactions (the symbols: LIi, LIVi, LIIIi, LIIi, LIa, LIIIa, LIIa placed in appropriate parallelepipeds and four orthogonal projections of these L vectors (the symbols: LIi, LIVi, LIIIi and LIa) are placed on basic 0 σ plane (Io, IIo … quadrants of this plane), the magnitude of ϕ angle about 3400.
Figure 1a: Three dimensional (completely) 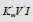 coordinate system, (the same as Figure 1), bat with all 14 branched L vectors
(7 type of additional L vectors placed without of appropriate arallelepipeds. The ends of all mobile L vectors are joined by
dash line (broken part – activated, unbroken part– L vectors of inhibited reactions). The 15th L0 vector of initial reaction (and
it L0 projection take place in P point of coordinate intersection. The all 14 orthogonal LIi, LIVi … LIa , LIa projections of L vectors
on basic 0 σ plane, are placed completely in (Figure 2).
coordinate system, (the same as Figure 1), bat with all 14 branched L vectors
(7 type of additional L vectors placed without of appropriate arallelepipeds. The ends of all mobile L vectors are joined by
dash line (broken part – activated, unbroken part– L vectors of inhibited reactions). The 15th L0 vector of initial reaction (and
it L0 projection take place in P point of coordinate intersection. The all 14 orthogonal LIi, LIVi … LIa , LIa projections of L vectors
on basic 0 σ plane, are placed completely in (Figure 2).  quadrants of transient σ " plane,
VIIa/Vi σ and Va/VIIi σ – beginning and finishing ends of the line of orthogonal σ " transient plane projection on basic σ0 plane (in
Figures.1a and 2, market by broken lines), the magnitude of ϕ angle about 3400.
quadrants of transient σ " plane,
VIIa/Vi σ and Va/VIIi σ – beginning and finishing ends of the line of orthogonal σ " transient plane projection on basic σ0 plane (in
Figures.1a and 2, market by broken lines), the magnitude of ϕ angle about 3400.
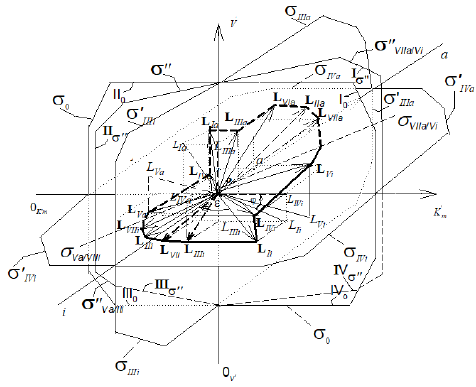
Figure 2: Two-dimensional (scalar) 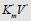 coordinate system. The symbols of kinetic parameters:
coordinate system. The symbols of kinetic parameters: 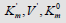 the projections LIi, LIVi… LIa, LIVa of three-dimensional vectors: LIi, LIVi… LIa, LIVa on the basic 0 σ plane and symbols of
the projections LIi, LIVi… LIa, LIVa of three-dimensional vectors: LIi, LIVi… LIa, LIVa on the basic 0 σ plane and symbols of 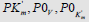 coordinate semiaxes the same as in Figure. 1 and in the text, the magnitude of ϕ angle about 150.
coordinate semiaxes the same as in Figure. 1 and in the text, the magnitude of ϕ angle about 150.
The Ii l length of LIi projection on 0 σ plane of Figures.; (1 - 2) may be determined as
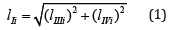
Having expressed from Eq. (2) the lIIIi length of LIIIi projection
of LIIIi vector on P0V semiaxis of 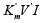 coordinate (Figures 1, 1a):
coordinate (Figures 1, 1a):

from Eq. (3) – the lIVi length of the second adjacent of LIVi vector
projection on 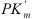 semiaxis:
semiaxis:
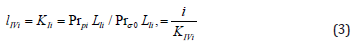
and substituted them in Eq. (4):

we shall obtain traditional form (t.f.) of equation for calculation of the Ii K constant of biparametrically coordinated, i I type, inhibition of enzymes, taking in to consideration the lIi length of orthogonal projection of LIi vector on basic 0 σ plane of Figure (1a):
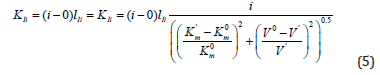
where 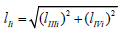 , as it follows from (Figures 1&2).
, as it follows from (Figures 1&2).
It is analogous for length of adjacent projections: 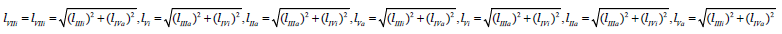 for all other lIIa, lVa … of vectors projections of biparametrical reactions (Figures 1,1a & 2).
for all other lIIa, lVa … of vectors projections of biparametrical reactions (Figures 1,1a & 2).
Deduction of Quadratic form of Equations
From analysis of Equations (1-4) one can easily see that substitution in Eq. (4) of the dimensionless coordinates of the lengths of LIIIi and LIVi vector projections is equal to substitution in this equation of the i /KIIIi and i /KIVi parameters then it is not difficult to become the alternative equations for calculation of i K and a K constants of biparametrical types of inhibition and activation of enzymes. Having substituted in Eq. (4) of the dimensionless coordinates of the lengths of LIIIi and LIVi vector projections is equal to substitution in this equation of the i /KIIIi and i /KIVi parameters.

we find that such as:

this substitution will lead to equation:
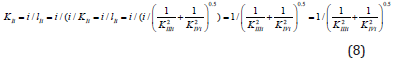
or, in quadratic form:
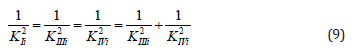
convenient for calculation of constant inhibition of enzymes (Eq. 1, q.f., in Table 1).
It is analogous for all the other equations of biparametrical
types of inhibition (Eqs: 2, 5 – 7), and activation (Eqs: 9 – 11 and
14-15 of enzymes, Table 1q & 1f) such as orthogonal projections of
correspond L vectors on the basic 0 σ plane, easy to determine by
data of two-dimensional (scalar) 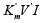 coordinate system (Figure
2), taking into account orthogonal L projections of tree-dimensional
L vectors on basic 0 σ plane of (Figures 1a).
coordinate system (Figure
2), taking into account orthogonal L projections of tree-dimensional
L vectors on basic 0 σ plane of (Figures 1a).
Examples of constants calculation.
Example 1: Calculation of Constant Inhibition
The inhibitory effect of Tungstic acid anions 2 4
4 WO − (0.5×10− M)
on the initial rate of pNPP cleavage by calf alkaline phosphatase
(Figure 3).
shows that the presence 0.5×10−4M of these anions in the
enzyme-substrate system makes the binding of the enzyme to the
substrate cleaved 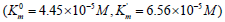 difficult
and leads to a decrease in the maximum reaction rate (V0= 2.56,
V’= 1.74μmol/ (min per μg protein). This meets all the features
difficult
and leads to a decrease in the maximum reaction rate (V0= 2.56,
V’= 1.74μmol/ (min per μg protein). This meets all the features  of the biparametrically coordinated, i I
type, of enzyme inhibition (Table 1, line 1). Hence, to calculate the
Ii K constant of this phosphatase inhibition it is necessary to use
Eq. (5, text), or (Eq. 1, Table 1t & 1f).
of the biparametrically coordinated, i I
type, of enzyme inhibition (Table 1, line 1). Hence, to calculate the
Ii K constant of this phosphatase inhibition it is necessary to use
Eq. (5, text), or (Eq. 1, Table 1t & 1f).
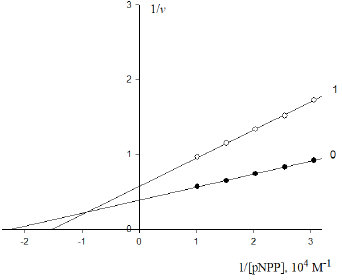
Figure 3: Inhibitory effect of anions 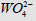 on the initial rate V0, mol/ (min per g protein) of pNPP cleavage by calf alkaline
phosphatase. Note: line 1 – the concentration of
on the initial rate V0, mol/ (min per g protein) of pNPP cleavage by calf alkaline
phosphatase. Note: line 1 – the concentration of 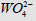 is 0.5×10−4M ; line (0) – the inhibitor is absent.
is 0.5×10−4M ; line (0) – the inhibitor is absent.
Substitution in this equation of the parameters 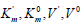 and i obtained by data analysis of (Figure 3) allows the calculation
of this constant of enzyme inhibition:
and i obtained by data analysis of (Figure 3) allows the calculation
of this constant of enzyme inhibition:
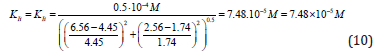
Substitution the same parameters (recalculated to values
of 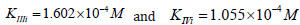 constants)
in equation (1 of Table 1t & 1f), result into next value of this Ii K
constant:
constants)
in equation (1 of Table 1t & 1f), result into next value of this Ii K
constant:
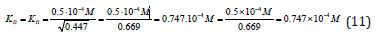
Substitution of these parameters in (Eq. 1, q.f., Table 1)
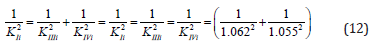
result into the same value of the constant of enzyme inhibition:
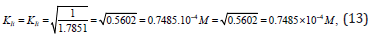
From Eqs. (10 -13) it follows that dimension of constants in all cases, are the molar concentration of inhibitor:

Control. Determine the value of the IIIi K constant of this experiment (Figure 3) by values of Ii K and IVi K constants.
From equations (11) and (12), rewritten to the form,
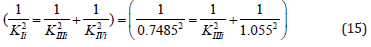
it follows that:

Substitution the necessary parameters from (Eq. 15) to (Eq. 16), we find that:
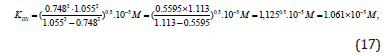
which is in good agreement with the experimental value of this constant (Eq. 12).
Example 2: Calculation of Constant Inhibition
The inhibitory effect of Pyrrolidine dithiocarbonic acid (PDTA)
on the initial rate of pNPP cleavage by canine alkaline phosphatase
shows that in the presence of 1×10−3M PDTA the parameters
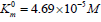 and V0= 2.921 μmol/(min per μg protein) change
as follows
and V0= 2.921 μmol/(min per μg protein) change
as follows 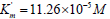 and V ' = 3.616 μmol/(min per μg
protein) (Figure 4). This corresponds to the, Vi type, of enzyme
pseudoinhibition
and V ' = 3.616 μmol/(min per μg
protein) (Figure 4). This corresponds to the, Vi type, of enzyme
pseudoinhibition  (Table 1, line 5) and
Eq. (5, t.f.) is applicable for calculation of the KVi constant of enzyme
inhibition. Substitution all necessary parameters in this equation
allows calculation of this constant of enzyme inhibition:
(Table 1, line 5) and
Eq. (5, t.f.) is applicable for calculation of the KVi constant of enzyme
inhibition. Substitution all necessary parameters in this equation
allows calculation of this constant of enzyme inhibition:
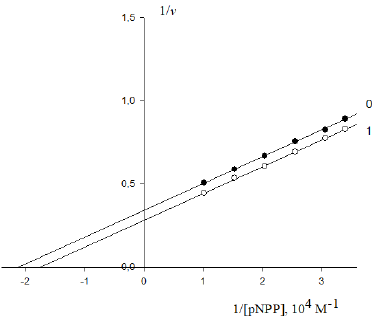
Figure 4: Inhibitory effect of PDTA on the initial rate V0 , mol/(min per g protein) of pNPP cleavage by canine alkaline phosphatase. Note: line 1 – the concentration of PDTA is 1×10−3M ; line (0) – the inhibitor is absent.
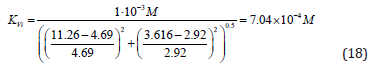
Substitution of recalculated parameters of (Figure 4) 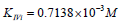 and
and 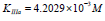 to (Eq. 5, Table 1, q.f.)
– result into value of Vi K constant inhibition:
to (Eq. 5, Table 1, q.f.)
– result into value of Vi K constant inhibition:
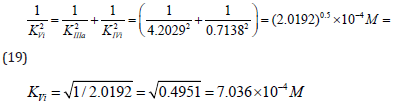
Example 3: Calculation of Constant Activation
The activating effect of Guanosine (Guo) on canine alkaline
phosphatase (Figure 5) shows that in the presence of 1×10−3M
Guo the parameters of initial reaction of pNPP cleavage, i. e 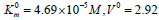 μmol/(min per μg protein), change as
follows:
μmol/(min per μg protein), change as
follows: 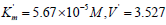 μmol/(min per μg protein).
This corresponds to the, Ia type, of unassociative enzyme
activation.
μmol/(min per μg protein).
This corresponds to the, Ia type, of unassociative enzyme
activation.
Figure 5: Activating effect of Guo on the initial rate v0, mol/(min per g protein) of pNPP cleavage by canine alkaline phosphatase. Note: line 1 – the concentration of Guo is 1×10−3M ; line (0) - the activator is absent.
Hence, to calculate the KIIa constant of enzyme activation, one should use Eq. (14, t.f., Table 1).
Substitution of the obtained values of parameters in this equation allows calculation of this constant of enzyme activation:
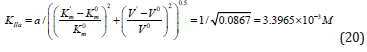
Substitution of the: 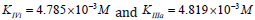 parameters of this experiment (Figure 5) in (Eq. 14, q.f., Table 1),
result in to:
parameters of this experiment (Figure 5) in (Eq. 14, q.f., Table 1),
result in to:
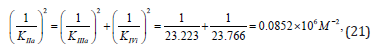
as it was to be expected, result in to the same value of activation constant:
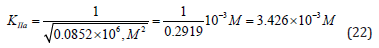
From the length parts of equations: (12), (15), (19) and (21) may to see that all they obeys to the signs of Pifagor’s theorem and this may be used as for calculation any of the third constants by the two others known already and for correction the constants, determined by using any other equations.
Example 4: Calculate the value of KIIIi constant of experiment (Figure 3), by value of KIi and KIVi constants. From equation (1, Table 1t & 1f), rewritten to the quadratic form (23).
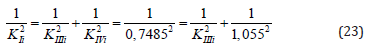
it follows that:

Having substitution all necessary parameters from (Eq. 23) to (Eq. 24), we shall become, that:
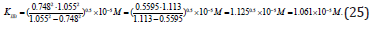
Ii is analogous for all biparametrically types of catalyzed reactions (Table 1).
Introduction in practice of quadratic forms of equations for calculation of Ki and Ka constants, will facilitates for many authors to interpret obtained data of nontrivial types of inhibition and activation by such definition as «essentially competitive inhibition», «similarly to competitive inhibition » and so on [13 -17].
References
- Krupyanko VI (2004) A vector method of representation of enzymic reactions. Three-dimensional system of the coordinates convenient for representation of enzyme inhibition and activation. Process Biochem 39 (7): 825-832.
- Кrupyanko VI (2009) Perspectives of Data Analysis of Enzyme Inhibition and Activation. Part 1: Use of the Three-Dimensional Coordinate System for Data Analysis of Enzyme inhibition and Activation. J Biochem Mol Toxicol 23(2): 97-100.
- Кrupyanko VI (2009) Perspectives of Data Analysis of Enzyme Inhibition and Activation. Part 2: Parametrical Classification of Types of Enzymatic Reactions. J Biochem Mol Toxicol 23(2): 101-107.
- Кrupyanko VI (2009) Perspectives of Data Analysis of Enzyme Inhibition and Activation. Part 3: Equations for Calculation of the Initial Rates of Enzymatic Reactions. J Biochem Mol Toxicol 23(2): 108-118.
- Кrupyanko VI (2010) Perspectives of Data Analysis of Enzyme Inhibition and Activation. Part 4: Equations for Calculation of Constants of Enzyme Activation and Inhibition. J Biochem Mol Toxicol 24(3): 145-154.
- Krupyanko VI (2014) Determination of intensity of enzyme inhibition and activation. Eur Chem Bull 3(6): 582-586.
- Krupyanko VI (2014) Non-existence of secondary coordinates of intersects. Eur Chem Bull 3(8): 815-822.
- Krupyanko VI (2015) Correction of Dixon Plots Eur Chem Bull 4(3): 142-153.
- Krupyanko VI (2016) Correction of Data Analysis Equations Relating to Two-Substrate Enzyme Catalyzed Reactions. Eur Chem Bull 5(8): 354-363.
- Webb L (1966) Inhibitors of Enzyme and Metabolism, [Russian translation], Mir, Moscow: pp:6 - 862.
- Segel IH (1975) Enzyme kinetics. J. Wiley, New York, pp: 1-957.
- Dixon M, aWebb EC (1982) Enzymes (2) [Russian translation], Mir, Moscow, pp: 6-862.
- Hovik R, Osmundsen (1989) HA kinetic investigation of the acyl-CoA oxidase reaction with the use of a novel spectrophotometric assay. Biochem J 263 (2): 297-299.
- Bae-Lee M, Carman GM (1990) Regulation of yeast phosphatidylserine synthase and phosphatidylinositol synthaseactiviteas by phospholipids in triton X-100/phospholipid mixed micells. J Biol Chem 265 (13): 7221-7226.
- Bakan DA, Saltman P, Theriault Y, Wright PE (1991) Kinetics and mechanisms of reduction of Cu(II) and Fe(III) complexes by soybean leghemoglobin a. Biochim Biophys Acta 1079(2): 182-196.
- Hou B, Lim EK, Higgins GS, Bowles DJ (2004) N-Glucosylation of Cytokinins by Glycosyltransferases of Arabidopsis thaliana. J Biol Chem 279(46): 47822-47832.
- Gibson LM, Lovelace LL, Lebioda L (2008) The R163K Mutant of Human Thymidylate Synthase 1s Stabilized on an Active Conformation, Structural Asymmetry and Reactivity of Cysteine 195. Biochemistry 47(16): 4636-4639.

 Mini Review
Mini Review