Introduction
The current study is an urgent warning on the Earth Day 2020 to prevent the blast of the COVID-19 pandemic to apocalypse. It is shown that the pandemic equations become unstable at reproduction numbers above 3.5, which could reflect in a chaotic catastrophe. There are many complex models describing pandemic kinetics [1,2]. In the current study we propose as chemists a minimalistic model based on chemical kinetics. Such type of equations describes different phenomena due to the universality of non-equilibrium thermodynamics developed by Onsager [3]. If X(t) is the fraction of infected people, its temporal dynamics will obey, the following nonlinear evolutionary equation
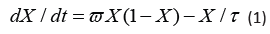
The first term on the right-hand side describes transfer of
coronavirus from infected to healthy people with a characteristic
frequency ϖ . Obviously, it corresponds to a second-order chemical
reaction, since there are two different sets of people. Meetings
among healthy or infected people do not affect the infection rate.
The other relaxational term in Eq. (1) is due to either recovery or
death of infected people and τ is the mean lifetime of infection. The
favorite solution of Eq. (1) is 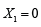 but there is another stationary
solution
but there is another stationary
solution 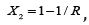 , which could be high at large reproduction
number R =ϖτ . The deterministic logistic function is the solution
of Eq. (1), which tends at large time to the healthy
, which could be high at large reproduction
number R =ϖτ . The deterministic logistic function is the solution
of Eq. (1), which tends at large time to the healthy 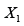 if
if 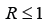 or
the pandemic
or
the pandemic 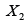 if
if 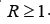 . The maximal infection rate appears in the
meddle at
. The maximal infection rate appears in the
meddle at 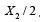 . One can recognize in Eq. (1) the well-known SIS
model from epidemiology.
. One can recognize in Eq. (1) the well-known SIS
model from epidemiology.
A peculiarity of the nonlinear Eq. (1) is the chaotic behavior.
Introducing the dimensionless time 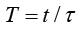 , being the natural
scale of the infection evolution, Eq. (1) can be rewritten as
, being the natural
scale of the infection evolution, Eq. (1) can be rewritten as
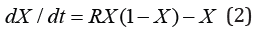
The discreetness of the society requires 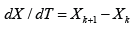 to be
expressed by a finite difference and in this case Eq. (2) reduces
straightforward to the standard logistic map [4,5]
to be
expressed by a finite difference and in this case Eq. (2) reduces
straightforward to the standard logistic map [4,5]
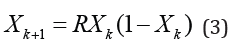
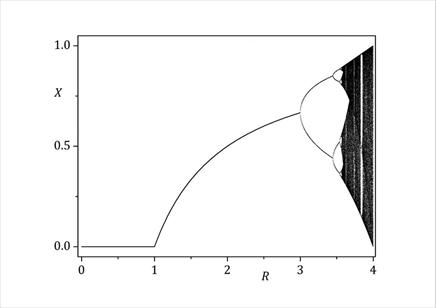
The bifurcation diagram of the map (3) shows at Figure 1 that
the pandemic solution 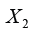 is unique in the range 1≤ R ≤ 3.
is unique in the range 1≤ R ≤ 3.
At larger reproduction number R > 3 a bifurcation hierarchy takes place [6]. Any bifurcation indicates oscillations between healthy-rich and infected-rich states, and this could trigger social segregation and confrontation. The onset of deterministic chaos at R > 3.5 marks the beginning of a cascade of chaotic apocalypses with unpredictable stochastic behavior. An unforeseen salvation is, however, that according to Figure 1 commensurable probabilities hold for the End ( X =1) and a new Beginning ( X = 0 ) at R = 4 . Though Einstein did not believe that God plays dice with the Universe, this would be the case here, because the logistic map has no solution at R > 4 .
Conclusion
The present study aims either educational or scientific goals. The used standard mathematical apparatus is well known in the classical theory of the chaotic systems and the paper is a useful demonstration how it could be applied to important living systems as well. The main contribution to science is the application to epidemiology. The traditional pandemic studies try to solve complex systems of nonlinear differential equations. Outstanding scientists have developed sophisticated models for precise predictions of pandemic but they never considered the bifurcation dynamics of their models. Indeed, the described SIS model is too simple to forecast the exact evolution of the COVID pandemic but we just wanted to stress that any epidemic model is non- linear, due to the infection spreading step, and this can result in a chaotic behavior. In conclusion, to fight effectively with the coronavirus epidemy people should try to reduce the reproduction number R =ϖτ either by suppressing ϖ via social distancing, masks and immunization, for instance, or by decreasing τ via advanced medical care. In any case R should be capped below 3.5 to prevent chaotic disasters. Of course, the present minimalistic model is oversimplified and its numerical predictions could be far from the reality. However, the exact models are even more nonlinear, which presumes a more complex chaotic behavior. But the World knew already that an apocalyptic pandemic was coming [7].
Acknowledgment
The author is thankful to Dr. V. Tonchev for inspiring discussions and grateful to Dr. A. Fauci and Dr. R.W. Eisinger for encouragement. Baron May of Oxford passed away at the day of the first publication of the paper online, R.I.P. Robert M. May [4].
References
- Daley DJ, J Gani (1999) Epidemic Modeling: An Introduction, Cambridge. In: Daley DJ, J Gani (Eds.)., Cambridge University Press, UK.
- Mollison D (1995) Epidemic Models: Their Structure and Relation to Data, Cambridge. In: Mollison D (Edt.)., Cambridge University Press, UK.
- De Goot SR, P Mazur (1962) Non-equilibrium Thermodynamics. In: de Goot SR, P Mazur (Eds.)., Dover Publications, New York, USA.
- May RM (1976) Simple mathematical models with very complicated dynamics. Nature 261: 459-467.
- Feigenbaum M (1978) Quantitative universality for a class of nonlinear transformations. J Stat Phys 19: 25-52.
- Robinson C (1999) Dynamical Systems: Stability, Symbolic Dynamics and Chaos. In: Robinson C (Edt.)., Boca Raton, CRC Press, USA.
- Garrett L (2019) The World knows an apocalyptic pandemic is coming. Washington Foreign Policy.

 Short Communication
Short Communication