Research ArticleABSTRACT
The rule of choice of equations for calculation of constants of enzyme inhibition and activation is proposed to prevent the unjustified use of these equations and expand the possibilities of their application for non-trivial data analysis in enzyme kinetics. Examples of use of equations are given.
Keywords: The rule of choice of equations for Ki and Ka constants calculation
Introduction
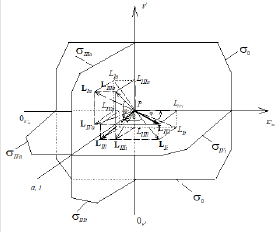
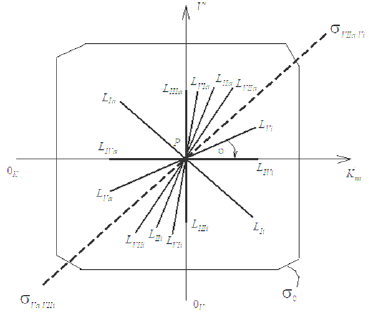
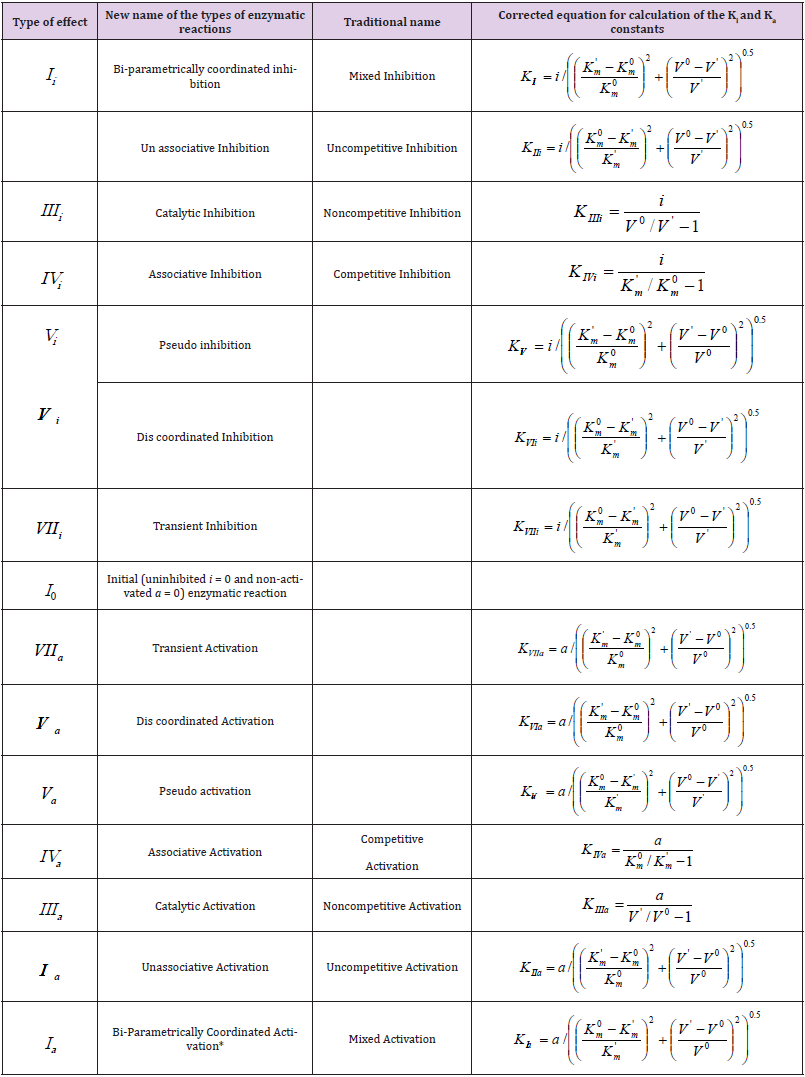
In previous works [1-5] the possibility of construction of L vectors of enzymatic reactions in the three-dimensional (packed) Km V I rectangular coordinate system (Figure 1) is considered. The taking into account of properties of L vectors, such as: symmetric position in the Km V I coordinate system and the ratio of l lengths of orthogonal projections on the coincident (Pa, i ) semi-axis to the ratio of the L vector projection on the semi-axis in basic s0 plane (Figure 2) permitted to construct a parametrical classification of the types of enzymatic reactions (Table 1) and correct the equations for calculation of the Ki and Ka constants of enzyme inhibition and activation, respectively, which now includes fourteen equations: 7 equations s for calculation of constants and 7 equations for calculation of Ka constants. It turned out that some of the obtained equations have similar algebraic forms, which required to consider the rule of choice of these equations to prevent their unjustified use and also for expansion of the possibilities of their application at data analysis in enzyme kinetics.
The rule of choice is considered in this work, and the examples
of using these equations for non-trivial data analysis in enzyme
kinetics are given, namely:
a) The cases, when the values of 
and V0 parameters of initial
reaction are absent
b) The cases, when there is possibility to use other equations
(similar in the form) for calculation of Ki and Ka constants and
c) The cases, when equations for calculation of monoparametrical
constants of enzyme inhibition are used for
calculation of bi-parametrical types of enzyme inhibition.
Figure 1: Three-dimensional (packed) Km V I system of rectangular coordinates with coincident Pi and Pa semiaxes (Pa,i) molar concentrations of inhibitor i and activator a .. The symbols of kinetic parameters: Km, V, 0m K …, three-dimensional vectors: LIi, LIVi… LIa, LIVa, and their projections LIi, LIVi… LIa, LIVa on the basic s0 plane as well as the symbols of projections of directing planes σIVi, σIIIi, σIVα, σIIIα on the PKm, P0V, 0Km P , и PV coordinate semiaxes the same as in the text and in [1-3].
Figure 2: Two-dimensional (scalar) Km V I coordinate system. The symbols of kinetic parameters: Km, V, 0m K …, the projections LIi, LIVi… LIa, LIVa of three-dimensional vectors: LIi, LIVi… LIa, LIVa on the basic s0 plane and symbols of PKm, P0v 0 Km P , и PV coordinate semiaxes the same as in Figure 1 and in the text.
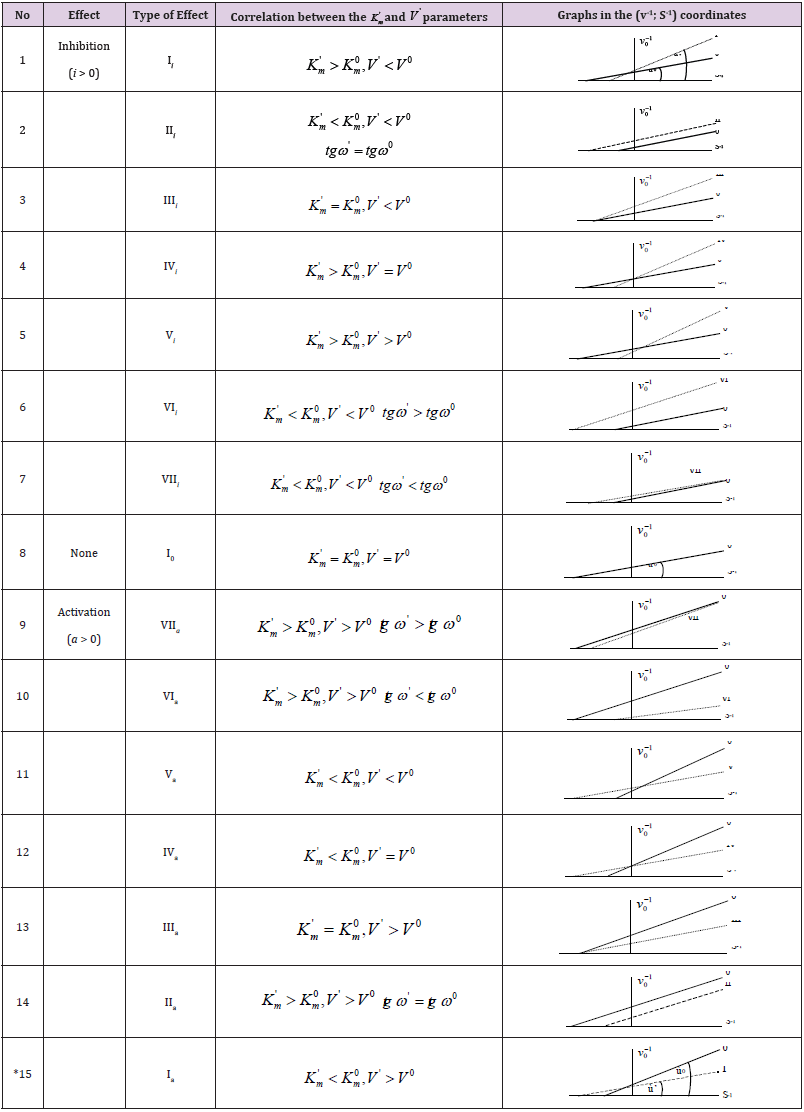
Table 1: Parametric classification of the types of enzymatic reactions.
Note: *The symbol of a graph in corresponds to the type of reaction under study. For example: the line (0) characterizes the position of initial (nonactivated) enzymatic reaction, line I – the position of a graph representing the Ia type of activated enzymatic reaction etc.
Materials and Methods
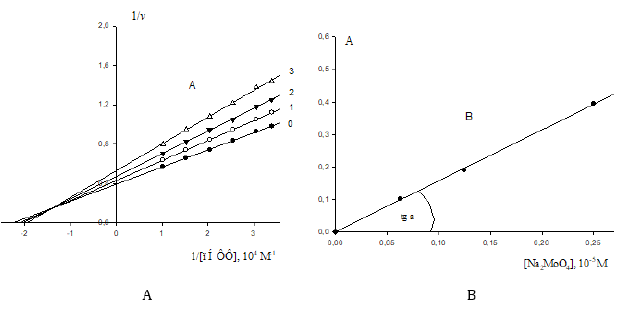
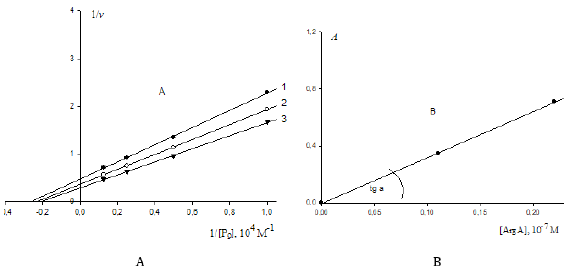
Calf alkaline phophatase (EC 3.1.3.1.) - a preparation of Sigma (USA). Substrate: p-Nitrophenylphosphate - 2CHA salt (pNPP) - a preparation of Serva (Germany). Enzyme inhibitor: Sodium molybdate (Na2MoO4×2Н2О) - a crystalline salt of high purity grade of domestic make. The cleavage of pNPP was recorded on a twobeam CF-4 DR spectrophotometer (Optica Milano, Italy). Reactions were carried out in 0.05M Tris-HCl buffer (pH 9.0) of ionic strength 0.1 by NaCl of high purity at constant mixing [1] in a thermostat at 37 0C. The curves of a course of reactions were registered by absorption increment (+ΔA400) of a solution containing the substrate, enzyme and inhibitor against the solution of the same composition, but without the enzyme. The concentration of pNPP was changed 0.294·10-4 – 0.98∙10-4M, the enzyme concentration was 1.96mg/ml (Figure 3A). The initial reaction rates (v) were determined by the slope angle of tangents to initial segments of curves of the course of a reaction in not less than 5 parallel experiments. The kinetic and parameters were calculated by plots in the (v-1 S-1) coordinates by Lineweaver-Burk using the program SigmaPlot, version 2000 (USA). The isolation of vacuolar polyphosphate hydrolase from N. crassa (EC 3.6.11) and the study of effect of arginine-containing activator (ArgA) on initial rates of P9 polyphosphate by this enzyme (Figure 3A) are given in [6]. Root-mean-square deviation at fivefold determination was: v = ± 2,5%, Km and V = ± 7,5%, Ki and Ka = ± 10%.
Figure 3:
A. Lineweaver-Burk plots of inhibitory effect of anions 2
4 MoO − (10-5М): 0.0625 – line 1; 0.125 – line 2 and 0.25 – line 3 on
initial rates of pNPP by calf alkaline phosphatase. Line 0 – the inhibitor is absent. Designation v, mmol/(min×per mg of
enzyme).
B. Dependence of change in values of (A) denominator of Eq. (1) (Table 1) upon increasing concentrations of Na2MoO4 in
coordinates (А;i). The concentration of Na2MoO4 (10-5 M): 0.0625, 0.125 and 0.25: 0.0625, 0.125 and 0.25, respectively.
Results and Discussion
Example 1
As seen in Table 1, the rule of choice of equations for calculation
of constants of enzyme inhibition and activation presupposes the
construction of experimental dependencies of change of vi initial
rates of inhibited (or activated va) reactions upon concentrations
of substrate cleaved S obtained in the presence of inhibitor i (or
activator a ) relative to the same rates of v0 initial (uninhibited i =
0 and non-activated a = 0) reaction in the v-1 S-1 coordinates. The
type of reaction is determined by the position of obtained plots and
according to the type – the equation for calculation of the respective
constant. However, great difficulties arise in the following cases
according to the forms of equations of Table 1, to calculate the
constants of enzyme activation,
1) It is necessary to obtain the values of not only Km and V
parameters of activated (or inhibited) reaction, but also the values
of and V0 parameters of initial (non-activated a = 0) reaction.
It can evoke difficulties at using equations of such data analysis,
because in some studies the values of and V0 parameters are
absent, for example, due to bad capability of the enzyme to cleave
substrate in the absence of activator. Such cases are often found in
laboratory practice [6-11], see, for example, the results of study
of activating effect of arginine-containing activator ArgA on initial
rates of P9 polyphosphate cleavage by vacuolar polyphosphate
hydrolase of N. crassa (Figure 3A). From these data it ease to see,
that the values of and V0 parameters of initial reaction in
this case are not determined. In some other cases the values of and V0 parameters of activated reactions there are ability to
determine [12-14]. The same situation also occurs at calculation
of Ki constants of enzyme inhibition, if the values of and V0
parameters of initial reaction are not determined [8,15]. Let us
examine Figures 3A & 3B devoted to study of enzyme inhibition by calf alkaline phosphatase (EC 3.13.1.) by increasing concentrations
of 
.
The values of and V0 parameters were not determined
in this case. According to the parametrical classification (Table 1,
line1) the data of Figure 3A correspond to the, i I , type of enzyme
inhibition [2, 3]. Using Eq. (1 of Table 1), the values of constants
of enzyme inhibition were calculated by each of 3 concentrations and the average value of Ii K = 0.628×10-5М constant
of alkaline phosphatase inhibition was estimated by the slope angle
(tg a) of experimental line (Figure 3B) to the abscissa axis in the
coordinates (A; i):
where (A) is the denominator of Eq. (1, Table 1). As easily
seen in Figure 3B, the value of constants of alkaline phopsphatase
inhibition can also be calculated by any intervals of inhibitor
concentrations, i.e. by the slope angle (tg a) to the abscissa axis of
respective segments of the experimental line without introduction
of additional symbols to 
parameters of Eq. (1)
(Table 1), namely, by having determined the values of 
and
V' parameters obtained, for example, by the 1st concentration of
inhibitor 0.0625 10-5 М and substituted them in Eq. (1) (instead
of and V0 parameters), and the values of and V'
parameters obtained by the 2nd concentration of enzyme inhibitor
0.125 10-5М – instead of and V' parameters (already available
in the equation). In this case, we shall obtain that for the interval of
inhibitor concentrations i2 - i1 = Δ i = (0.1255 - 0.0625) 10-5 М =
0.0625 10-5 М
Yet, here it is more advisable to calculate the Ii K constant of
enzyme inhibition by the slope angle of the plot (Figure 3B) to the
abscissa axis ( Ii K = 0.6291⋅10-5М). As seen in (the Figure 3B), the
removal of the zero point ( = 0 и V0 = 0) on the plot in this case
(the absence of really great deviation in the values of denominators
of Eq. (1) (Table 1) will be not exhibited by any change of the slope
angle of the plot to the abscissa axis.
Example 2
Use of this technique (Example 1) to data analysis (Figure 4A), which now taking into account the above-said can be referred to the a VI type of polyphosphate hydrolase activation – leads to calculation of the following values of the constants of enzyme activation (Eq. 6, Table 1): VIa K = 3.182 (μM) – by the interval ArgA (2.2 - 1.1 = 1,1) μM and VIa K = 3.103 μM – by the interval ArgA (3.3 - 1.1 = 2.2) μM). The construction of dependencies of A denominators (Eq. 6) upon the intervals of ArgA concentrations in the coordinates ( A, Δa ) (Figure 4B), where the slope angle (tg a) of the plot to the abscissa axis according to Eq. (6, Table 1) is connected with the value of VIa K constant of enzyme activation by a ratio:
Figure 4:
A. Activating effect of ArgA on initial rates VIIa v of P9 polyphosphate cleavage catalyzed by vacuolar polyphosphatase
from N. crassa: lines 1, 2 and 3 – the concentration of ArgA is: 1.1μM – line 1; 2.2μM – line 2 and 3.3μM – line 3. Designation:
v – μE/min.
B. Dependence of change in the A denominators of Eq. (6) (Table 1) upon increasing concentrations of ArgA in the
coordinates (А; ). The intervals of ArgA concentrations are 1.1μM and 2.2μM , respectively.
Bearing in mind that the parameter b(1) of the computing program Statistics (SigmaPlot, version 2000) characterizes the value of the same slope angle (tg a) of the plot (Figure 4B) to the abscissa axis, one can calculate the value of the target constant of enzyme activation by a ratio:
Example 3
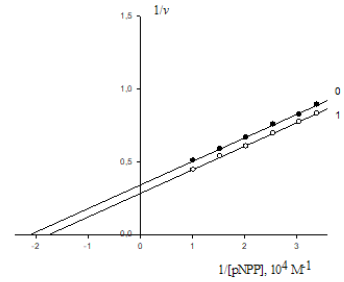
Calculation of constant activation. The activating effect of
Guanosine (Guo) on canine alkaline phosphatase (Figure 5) shows
that in the presence of 1×10-3М Guo the parameters of initial reaction
of pNPP cleavage, i. e. = 4.69×10-5M, V0 = 2.921mmol/min per mg
protein, change as follows:
= 5.67⋅10-5М, V = 3.3527 mmol/min
per mg protein. This corresponds to the IIa type of un associative
enzyme activation. Hence, to calculate the constant of enzyme
activation, one should use Eq. (14, Table 1). Substitution of the
obtained values of parameters in this equation allows calculation of
this constant of enzyme activation:
Note: line 1 – the concentration of Guo is 1⋅10-3M; line (0) – the activator is absent.
Figure 5: Activating effect of Guo on the initial rate 0 v , μmol/min per μg protein of pNPP cleavage by canine alkaline phosphatase.
Substitution of the: IVi K = 4.785٠10-3M, KIIIa = 6.76٠10-3M parameters of this experiment (Figure 5) in (Eq. 14, [16]), result in to:
substitution in (Eq. 6), rewritten to the form:
result in to the same value of activation constant:
From the length parts of equations: (6) и (7) may to see that all they obeys to the signs of Pifagor’s theorem and this may be used as for calculation any of the three constants by the two others known already and for correction the constants, determined by using any other equations. For example for calculation any of the third constants by the two others known already, or for correction the constants, determined by using any other equations. This extremely convenient in many other cases. Namely, from (Eq. 8) it follows that:
Having substituting the all necessary parameters in Eq. (9), we will become that,
and as it was to be expected, this result in to the same value
of constant ( KIVi = 4.785٠10-3M). But by use KIIIa = 6.76٠10-3M,
(consider that = ) [17-21] IVi K = 4.785٠10-3M (consider
that V' = V0 ) [21-23], or we shall become / IVi IIa K K = 4.785/3.904,
more than 22%; / IIIa IIa K K = 6.76/3.904 more than 72%.
Discussion
As easily to see by comparison of Eqs. (4, 1 and 5) (Table 1) that
the value of IVi K constant of enzyme inhibition can be estimated
not only using Eq. (4), but also by Eq. (1) and Eq. (5 of Table 1),
which (if the ratio of parameters = ) will be simplified to
Eq. (4). To explain the above situation, it is convenient to consider
Figure 2, where the positions of LIVi, LIi, and LVi projections of
respective vectors of reaction under study on the basic s0 plane of
Figure 1 are given. As seen in Figure 2, the = projection
of LIi of vector and LIi projection of LVi of LVi of vector will occupy
the place of LIVi projection of LIVi vector of inhibited reaction at
the ratio of parameters …, i.e. the mono-parametrical, IVi type, of
enzyme inhibition is transient between Ii and Vi bi-parametrical
types of enzyme inhibition. Evidently use of Eqs. (1 or 5 of Table
1) for calculation of the constant of enzyme inhibition will lead to
correct calculation of their values. It is not recommended to make
such substitution of equations due to the following reasons:
1) Substitution of Eq. (4) by Eqs. (1 or 5) will not simplify the
calculation of IVi K constant, but
2) The form of equation and the symbol of constant, if not
corrected, may disorient the reader and orient to choose type IVi
instead type Ii of enzyme inhibition.
It is analogous in the case of using the other equations for
calculation of Ia K and IIa K Va K , VIa K and VIIa K bi-parametrical
constants activation: see Eqs. (15, 14, 11, 10 and 9 of Tables 1 &
2) and the positions of respective bi-parametrical: LIa, LIIa, LVa …
projections of three-dimensional LIa, LIIa, LVa … vectors relatively to
LIVa, LIIIa, LIVi and LIIIi projections of (two-parametrical LIVa, LIIIa, LIVi
and LIIIi vectors) among their surroundings (Figures 1 & 2).
Table 2: Equations for calculation of the Ki and Ka constants.
References
- Krupyanko VI (1990) A Vector Method of Representation of Enzymic Reactions. Moscow: Nauka, pp. 3-142.
- Krupyanko VI (2009) Perspectives of Data Analysis of Enzyme Inhibition and Activation. Part 2: Parametrical Classification of Types of Enzymatic Reactions. J Biochem Mol Toxicol 23(2): 101-107.
- Krupyanko VI (2010) Perspectives of Data Analysis of Enzyme Inhibition and Activation. Part 4: Equations for Calculation of Constants of Enzyme Activation and Inhibition. J Biochem Mol Toxicol 24(3): 145-154.
- Krupyanko VI (2014) Non-existence of secondary coordinates of intersects. Eur Chem Bull 3(8): 815-822.
- Krupyanko VI (2015) Correction of Dixon Plots. Eur Chem Bull 4(3): 142-153.
- Vagabov VM, Trilisenko LV, Krupyanko VI, Il chenko VI, Kulaev IS (1990) Intracellular arginine activates of polyphosphohydrolase from Neurospors krassa? Proceedings of Academy of Sciences of the USSR 311(4): 991-994.
- Monder C, Lakshmi V, Miroff Y (1991) Kinetic studies on rat liver 11 -hydroxysteroid dehydrogenase. Biochim Biophys Acta 1115(1): 23-29.
- Podshun B, Cook PF, Schnackerz KD (1990) Kinetic mechanism of dihydropyrimidine dehydrogenase from pig liver. J Biol Chem 265(22): 12966-12972.
- Shi Y, Jiang Z, Han P, Zheng GX, Song KK, et al. (2007) Purification and some properties of b-N-acetyl-D-glucosaminidase from the cabbage butterfly (Peris rapae). Biochemie 89(2): 347-354.
- Lin Y, Alguindigue SS, Volkman J, Nicholas KM, West AN, et al. (2007) Complete Kinetic Mechanism of Homoisocitrate Dehdrogenase from Saccharomces cerevisae. Biochemistry 46(3): 890-898.
- Hara A, Shinoda M, Kamazu T, Nakayama T, Deyashiki Y, et al. (1991)Inhibition of dimeric dehydrodiol dehydrogenase of rabbit and pig lens by ascerbic acid. J Biochem 275(1): 121-126.
- Smith CA, Rangarajan M, Hartley BS (1991) D-xylose (D-glucose) isomerase from Arthrobacter strain N.R.R.I. B 3728. Purification and properties. Biochem J 277(1): 255-261.
- Edelberg JM, Weissler M, Pizzo SV (1991) Kinetic analysis of the effects of glycosaminoglycans and lipoproteins on urokinase mediated plasminogen activiton. Biochem J 276(3): 785-791.
- Bae Lee M, Carman GM (1990) Regulation of yeast phosphatidylserine synthase and phosphatidylinositol synthase activite as by phospholipids in triton X-100/phospholipid mixed micells. J Biol Chem 265(13): 7221-7226.
- Hoimsen H, Storm E (1969) The Adenosine Triphosphate Inhibition of the Pyruvate Kinase Reaction and its Dependence in the Total Magnesium Ion Concentration. Biochem J 112(3): 303-316.
- Krupyanko VI (2007) Corrected Equations for Calculation of Constants in Enzyme Inhibition and Activation. Biochemistry (Moscow) 72(4): 380-391.
- Tanizaki MM, Bittencourt HMS, Chaimovich H (1997) Activation of low molecular weight acid phosphqatase from bovine brain by purines and glycerol. Biochim et Biophys Acta 485(1): 116-123.
- Godeau JM (1980) Arginyl Transfer Ribonucleic Acid Synthetase of B. stearothermophillus Purification and Kinetic Analysis. Eur J Biochem 103(1): 169-177.
- Abou Zeid AM, Jerebzoff S, Jerebzoff Quintin S (1991) Alanine aminotransferase in Leptosphaeria michott. Isolation, properties and cyclic variations of its activity in relation to polypeptide level. Physiologia Plantarum 82(3): 401-406.
- Rose ZB, Grove DS, Seal SN (1986) Mechanism of activation by anions of phosphoglycolate phosphatases from Spinach and Human red blood cells. J Biol Chem 261(24): 10996-11002.
- Hara A, Shinoda M, Kamazu T, Nakayama T, Deyashiki Y, et al. (1991) Inhibition of dimeric dehydrodiol dehydrogenase of rabbit and pig lens by ascerbic acid. J Biochem 275(1): 121-126.
- Smith MA, Kannangara C, C Grimm B, Wettstein D (1991) Chracterization of glutamate-1-semialdehyde aminotransferase of Syneohoccus. Eur J Biochem 202(3): 749-757.
- Lai H Ch J, Gia B, Tu Ch (1989) Characterization of a Variant Rat Glutation S-Transferase by cDNA Expression in E. coli. Arch Bioch Biophys 273(2): 423-432.
