Abstract
The use of an Alternating Magnetic Field (AMF) to Magnetic Nanoparticles (mNPs) is currently being investigated as a technique for selective therapeutic heating of tumors. Different forms of superparamagnetic and ferromagnetic particles, as well as different coatings and targeting agents, can be used to target tumor locations. In this paper, Brown’s continuous diffusions model [1] of magnetization is used to treat the Magnetic Hysteresis Loops (MHL) of a ferromagnetic nanoparticle subjected to external ac fields. In contrast to uniaxial particles, magnetic hysteresis is strongly influenced by the ac magnetic field.
Keywords:Ferromagnetic Nanoparticles; Magnetic Hysteresis Loops (MHL); Biaxial; Susceptibility
Abbreviations: AMF: Alternating Magnetic Field; mNPs: Magnetic Nanoparticles; MHL: Magnetic Hysteresis Loops; MHP: Magnetic Hysteresis
Mini Review
Due to both fundamental aspects of their magnetization and growing industry [2] interest, especially in data storage [3], fine single domain ferromagnetic nanoparticles have been a hot topic of research for more than 60 years. Medical applications, such as hyperthermia [4], are also significant in the present. The instability of magnetization [5] M(t). is a function of such nanomaterials, like superparamegnetic nanoparticles, the phenomenon of superparamagnetism [5] is caused by thermal agitation resulting in spontaneous change of orientation from one metastable state to another by surmounting Zeeman energy barriers [6]. Because single-domain nanoparticles have a large magnetic dipole moment, the Zeeman energy is relatively high even in weak external magnetic fields, the field dependence of the magnetization reversal process causes nonlinear effects in dynamic susceptibility, stochastic resonance, dynamic Magnetic Hysteresis (MHP), and other phenomena. The calculation of the nonlinear response of the magnetization in the presence of the thermal is required to determine the nonlinear magnetic susceptibility and MHP for arbitrary ac field strengths. This calculation is typically handled by the Langevin equation, which is Gilbert’s [7] (or Landau- Lifshitz’s [7]) equation augmented by a random field h(t) with Gaussian white noise properties, accounting for thermal fluctuations in an individual particle’s magnetization.
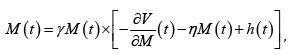 (1)
(1)where is the gyromagnetic ratio, is the damping parameter, and V is the free energy per unit volume consisting of the magnetic anisotropy Hamiltonian and Zeeman energy densities. The saturation magnetization is assumed to be constant in this case, so the only variable is the orientation of M. The azimuthal and polar angles of the spherical polar coordinate system give the orientation of M(t). This equation is then used to derive the associated Fokker- Planck [6] equation (FPE) governing the time evolution of the probability density function of magnetization orientations on a sphere of radius (u is a unit vector along M), and the relevant FPE is given [1].
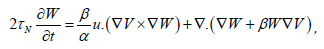 (2)
(2)where ∇ = ∂ / ∂u is the gradient operator on the unit sphere, s α =γηM is the damping, τN =τ0( α +α−1) is the typical free diffusion time of M(t), and τ0 = β Ms/ (2γ) , β = v / (ΚΤ) , v is the volume of the particle, k is Boltzmann’s constant, and T is the temperature. Various treatments of the nonlinear ac stationary response have been carried out by employing numerical solutions to the governing dynamical equations (1) and/or (2). In particular, efficient numerical algorithms for calculating the nonlinear ac stationary response of uniaxial systems are being developed superparamagnetic nanoparticles have been proposed (see, for example,) by assuming that the ac driving field is directed along the particle’s easy axis. However, because there is no dynamical coupling between the longitudinal and transverse modes of motion in this axially symmetric configuration, many interesting nonlinear effects cannot be treated or understood. These results have recently been generalized to determine the nonlinear ac stationary response for a uniaxial particle driven by a strong ac field applied at an angle to the particle’s easy axis, so that the axial symmetry is broken by the Zeeman energy. Only the axially symmetric uniaxial anisotropy potential has been treated in the preceding papers, greatly simplifying the analysis. The results, however, cannot be applied to particles that have inherent nonaxially symmetric anisotropy, such as biaxial (orthorhombic) anisotropy [8].
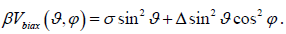 (3)
(3)Here, Δ and σ are the biaxiality and barrier parameters, respectively Δ = 0 corresponds to uniaxial anisotropy),ϑ and ϕ are polar and the azimuthal angles of the spherical coordinate system. We treat this problem because biaxial anisotropy may yield an appreciable contribution to the free energy density of magnetic nanoparticles [9]. In particular, where, Δ and σ are the biaxiality and barrier parameters (corresponding to uniaxial anisotropy), respectively, and are the polar and azimuthal angles of the spherical coordinate system. We address this issue because biaxial anisotropy can contribute significantly to the free energy density of magnetic nanoparticles. specifically. Titov, et al. [10]. presented a method for solving the general nonlinear problem [i.e., nonlinear ac stationary response for superparamagnets with arbitrary anisotropy and including the gyromagnetic term in the FPE (2)]. Using this method, we calculate the nonlinear magnetic susceptibilities and MHP of nanoparticles with biaxial anisotropy when subjected to a strong alternating current field. We will show that for arbitrary ac and dc bias field orientations, the magnetization dynamics change significantly, resulting in new temperature and damping dependent nonlinear effects at low, mid, and high frequencies.
Mathematical Model
In superimposed homogeneous external magnetic dc and ac fields of arbitrary strengths and orientations, the free-energy density V of a single-domain ferromagnetic nanoparticle with biaxial anisotropy is given by [11]
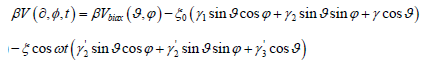 (4)
(4)where ξ0 = βH0Ms, ξ = βHMs , MS is the saturation magnetization,
γ1 = sinψ cosφ ,γ2 sinψ sinφ ,γ3 = cosψ
and 'γ1 , 'γ2, 'γ2 are the vectors H0 and H direction cosines, respectively.
As demonstrated in Ref. 20, the solution of the Gilbert-Langevin equation (1) for any anisotropy potential can be reduced to an infinite hierarchy of differential-recurrence equations for the statistical moments governing magnetization dynamics. ( ϑ , ϕ ) Ylm is a spherical harmonic of order l and rank m defined as [9]
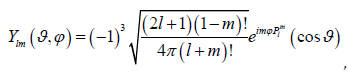
where Pml (x) denotes the Legendre functions.
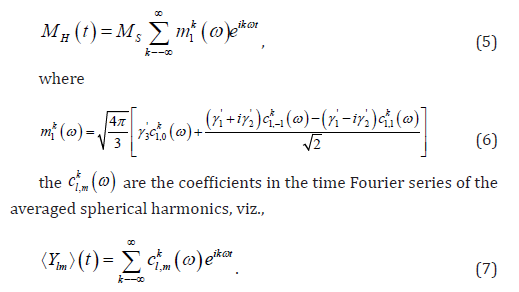
We obtain the ac stationary solution for magnetization MH (t ) in the direction of the ac driving field H by using generalized differential-recurrence equations specialized to biaxial nanoparticles, viz. [9],
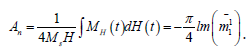
Using matrix continued fractions, the coefficients ckl m (ω), and thus the magnetization, MH(t) can be calculated (see Appendix). We will consider the parameter rangeσ >>1 and ξ ≥1 corresponding to the low temperature limit and strongly nonlinear regime when calculating the nonlinear ac response. Assume that the vectors H0 and H are parallel and that they lie in the XZ(φ = 0) or YZ(φ =π / 2) or YZ (φ =π / 2) planes of the laboratory coordinate system, so that the direction cosines are γ1 = sinψ or γ2 = 0 , γ3 = cosψ or γ1 = 0 , γ3 = cosψ , or respectively, whereψ is the polar angle between H and the Z axis taken as the particle’s easy axis. The MHP loop now represents a parametric plot of the steady-state timedependent magnetization as a function of the AC field, i.e.MH(t) vs. H (t ) = H cosωt , vs. H (t ) = H cosωt , where the time interval t coincides with the field’s period of oscillation for a given value of. The normalized area of the MHP loop n A (which is the energy loss per particle and per cycle of the AC field) is defined as 9 in this case [12].
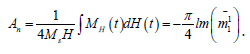 (8)
(8)Results and Discussion
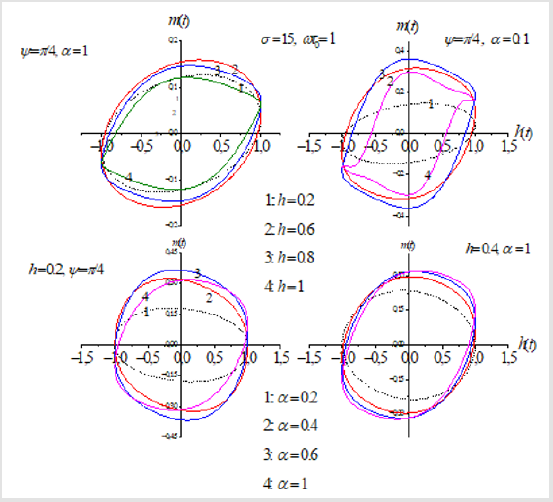
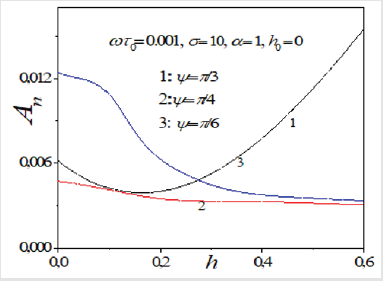
MHL loops for various ac field amplitude, damping, and dimensionless barrier parameter σ ∝1/ T values are shown in Figure 1. The size of the cycles changes as the biaxial parameter changes, as shown in Figure 1. Furthermore, the coercivity, remanent magnetization, and saturation magnetization are all strongly dependent on the barrier height, resulting in significant variation in the size and shape of loops for different values of σ at low frequencies. As a result, the magnetic response remains strongly temperature dependent. All of the hysteresis loops for ωτ0 =1, α =10−1 , ξ0 = 0 , andσ ≥ 5are large, retaining a large fraction of the saturation field when the driving field is removed. For σ ≥ 2 , we have narrow hysteresis loops, implying that reversing the magnetization repeatedly consumes a small amount of energy. In contrast to uniaxial particles, the MHL is clearly shown in Figure 1 to be strongly dependent on azimuthal direction. Figure 2 shows that the MH loops and normalized loop area are strongly dependent on the biaxial parameter, the oblique angle, the damping, and the dimensionless frequency, indicating that thermal fluctuations are primarily responsible for magnetization relaxation. The dynamic hysteresis at high frequencies, such as ωτ0 =1 Figure 2, is caused by resonant absorption in the FMR band. Thus, the MHL resulting from a high-frequency periodic signal can be evaluated, allowing for quantitative analysis of ultrafast magnetization switching.
Figure 1: MHL loops at ωτ0 =1 for barrier parameter σ =10 , for various damping, and various ac field parameter h, dc field and various damping α = 0.2,0.4,0.6,1,.
Figure 2: Area of the MHL An as functions of the parameter of the alternative field h for different value of damping (a) α =1,0.1,0.01, dc field parameter ξ0, ωτ0 =10−3, and different values of the barrier (b) σ = 5,10,15 frequency ωτ0 =10−1 and various barrier parameters σ , and ψ angles.
Conclusion
Brown’s model has been used to provide a rigorous treatment of the dynamic hysteresis loops of a single domain particle with biaxial anisotropy. All calculations were performed with the system initially assumed to have biaxial anisotropy, and no approximations were used other than those already inherent in Brown’s model. The current calculation, which involves both alternating and direct current fields applied at arbitrary angles to the easiest axis of magnetization (taken as the polar axis) in a bistable system, is the first attempt to treat an anisotropy that is not uniaxial in this manner. Titov et al. provided detailed treatments of the same problem restricted to uniaxial anisotropy for both an ac field and a dc field of arbitrary strength applied at angles to the easy axis of magnetization.
Acknowledgment
We thank. Prof. Titov for useful comments.
References
- Brown WFJr (1963) Thermal Fluctuations of a Single-Domain Particle. IEEE Trans. Mag 15: 1196 (1979). Phys Rev 130(5).
- Hilger WA, Kaiser, Magn J (2004) Pankhurst AN K. Mater 280: 358.
- Hergt R, Hiergeist R, Zeisberger M, Glockl G, Ramirez LPI, Weitschies W.
- Lacroix LM, Lachaize S, Malaki RB, Carrey J, Respaud M, et al. (2009) J Appl Phys 105: 023911. Carrey J, Mehdaoui B, Respaud M (2011) J Appl Phys 109: 083921. Usov NA, Ya B, Liubimov (2012) J Appl Phys 112: 023901.
- Bean CP, Livingston JD (1959) Journal of Applied Physics 30: 120S.
- Gilbert TL (1956) Physical Review 100: 1243.
- Landau LD, Lifshitz EM (2000) Mechanics (3rd)., (Pergamon Press), London, UK.
- Yu P, Kalmykov, Ouari B (2005) Phys Rev B 71: 094410.
- Coffey WT, Yu P, Kalmykov (2012) The Langevin Equation (3rd)., (World Scientific), Singapore.
- Titov SV, Déjardin PM, Mrabti HEI, Yu P (2010) Kalmykov Phys Rev B 82: 100413(R).
- Madani M, Ouari B (2020) Journal of physics and optics sciences 2: 3-4.
- Raikher YL, Stepanov DVI (2004) Adv Chem Phys 129: 419.

 Mini Review
Mini Review