Mini ReviewAbstract
Exact dose delivery to cancer patients in their treatment by radiation is very important. Radiation Dosimetry is a specific area in which exact dose calculation to patients and radiations workers is performed before any dose delivery. A cancer patient can be exposed to radiation in two ways: external exposure and internal exposure. External exposure occurs when source of radiation is located and placed outside a patient. Internal exposure is due to radiopharmaceuticals taken inside a patient’s body. The area of dosimetry dealing with radiation delivered by external sources of radiation is called external dosimetry and the area in which radiation is obtained from radioactive sources within the body is called internal dosimetry. In this minireview, various methods and systems used in the internal dosimetry are analyzed. Comparison of those methods reveals that every method and system has its own advantages and priorities over others in various cases and circumstances.
Keywords: Dosimetry; Internal Dosimetry Methods; Internal Dosimetry Systems
Abbreviation: S: Source Organ; CFR: Code of Federal Regulations; GI: Gastrointestinal Tract; ALI: Annual Limit of Intake, DAC: Derived Air Concentration; ICRP: International Commission on Radiology Protection
Mini Review
This different internal dosimetry methods were developed for the purpose of radioprotection, and radiation safety to minimize the risk of the effects of ionizing radiation on the people. The current method for calculating dose was proposed by the ICRP [1-4]. Internal dosimetry modalities or methods are used when a radioactive material enters the body by different routes inhalation, ingestion, absorption, injection on different circumstances either by breathing, eating, or drinking respectively, contaminated air, fluids foods and wounds. These occur in different occasions, either occupational or accidentally. In this course class paper, we describe the various mathematical models for calculating the absorbed dose by diverse organs of the body.
Internal Dosimetry Dose Calculation
The quantification of the absorbed dose to tissue requires the amount of energy deposited per unit mass of the body tissue. That energy comes from different type of radiations, the penetrating emissions (x and γ-rays), as well as non-penetrating ones α and β. Furthermore, the radiation absorbed dose is a function of lot of parameters such as: the activity of the radionuclide, its physical and biological half-life Tp and Tb, the fractional abundance of the radiation with energy Ei emitted per nuclear transition ni, the fraction of energy emitted that is absorbed in the target volume ϕi, the pathology or biodistribution of the radioactivity in the body [5,6]. The equivalent and effective doses are proportional to the radiation and tissue weighting factors and the absorbed dose. The absorbed dose rate is given by the equation:
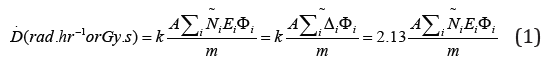
Where A ̃ [μCi or Bq], is the accumulated activity,
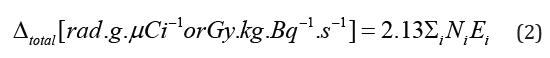
is the equilibrium absorbed dose constant, and , is the mass of the target volume. This formula is applicable only for nonpenetrating radiations (α-rays and β-rays), implying that all the energy is absorbed in the target volume. For penetrating radiations (x and γ-rays), all the energy or portion of it will be absorbed by the target volume. When the source and the target are different, we must insert a coefficient to account for the partial absorption of the energy by the target tissue, then, the absorbed dose is given by the following equation.
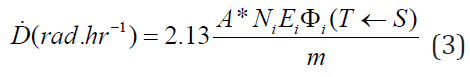
Where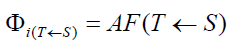 
is the absorbed fraction of dose
coming from the source organ (S), that is absorbed by the target
organ T. For α and β particles, x- and γ-radiation of energies less
than 11 keV, all the energy emitted. By the radiopharmaceutical is
absorbed in the volume greater than 1cm. So, ϕi will take the value
0, unless the source S and target T are the same, ϕi. For α and β
particles, most non-penetrating radiation is usually absorbed, so
we set the absorption fraction ϕi. For x and γ-rays, penetrating
radiation with energy greater than , the value of ϕi varies inversely
with increasing energy and between 0 and 1, contingent on the
energy. The data of ϕi are computed by statistical Monte Carlo
methods based on the interaction radiation and matter [6].
Different Dosimetry Systems
The previous formulas have been derived using lot of simplifications and are the most commonly used to calculate dose for radiopharmaceutical with complex emission spectra. These dosimetry systems that seem to look different, where some parameters have been combined, may look different, but yield the same output given the same input and assumptions.
Marinelli-Quimby Methods
The equation for the dose of non-penetrating beta (β) emitter that decays completely in a body tissue is given by the equation: [7,8].
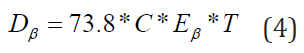
where: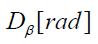 
is the concentration of the radionuclide,
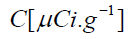is the concentration of the nuclide, 
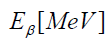is the
mean energy emitted per decay of the nuclide, is the half-life of
the nuclide in the tissue. By analogy with the cumulative activity,
0
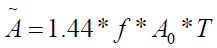,we see that 
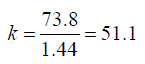, and
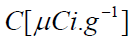is the
activity per unit mass, and for the β emitter, the absorbed fraction
ϕ=1. For penetrating radiations such as γ-rays, we use the geometric
factors of Brownell and Hine [9] for spheres and cylinders of set
shape to calculate the data for the fraction of energy ϕ emitted that
is absorbed in the target volume. The dose in the vicinity of the
γ-emitter is given by the formula:
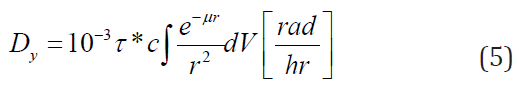
where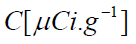 
is the activity of the gamma emitter. Similarly,
by analogy, the specific γ-rate constant Γ is the exposure rate per
disintegration from the point source (same as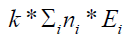 
) to an
infinite medium, while the factor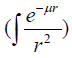 
plays a role of the absorbed
fraction, with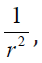 
being basically the absorbed fraction and μ is an
absorption coefficient.
International Commission on Radiology Protection (ICRP)
The ICRP introduced two methodologies ICRP II [10] and
ICRP 30 [1] for internal dosimetry implementable in occupational
settings, particularly in the nuclear fuel cycle with reference to
(Figure 1). The ICRP II is the foundation of the radiation protection
regulations in the US (Code of Federal Regulations (CFR), 10 CFR
20), which was revised (10 CFR 20) in 1994 and gave birth to the
new ICRP 30. The ICRP II and ICRP 30 systems have to do with
occupational exposure and its calculation of the dose equivalent
using the formula: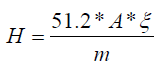 
, with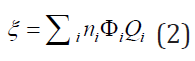 
Where ni,ϕi are defined in section 2., while Qi is the quality factor of the radiation to get the result in equivalent dose. The constant 5.12 is the k constant that converts into rem per day, for activity A(μCi), mass m(g), and energy E(MeV). At time t = 0, a certain amount of radiopharmaceutical enters the body either by inhalation or ingestion. For the gastrointestinal (GI) tract as well as the respiratory system models are used to compute the transfer of radionuclide from the GI or the respiratory system to the body fluids as well as its excretion. Then, by either pathway of intake, the radionuclide enters the body fluid system [11]. The radionuclide enters the body through compartment a which is connected to different compartments, b, c, d, etc. representing type of tissues or organs of the body, where the radiopharmaceutical experiences biological clearance and physical decay, and finally goes out of the body. The dose distribution in the first compartment is assumed to be uniform in the reference man. The ICRP metabolic design uses mathematical models for the reference man to track the radiopharmaceutical as it moves from the original compartment to other tissues or organs. The different compartment models are: ICRP-30 Dosimetric Model for Respiratory System (ICRP Human Respiratory Tract Model), ICRP-30 Dosimetric Model for the Gastrointestinal Tract, and ICRP-30 Dosimetric Model for Submersion in a Radioactive Gas Cloud. The solutions of these computations are the equivalent dose and effective dose rates of various tissues and organs as a function of time. Then, the committed equivalent dose and the committed effective dose subsequent from the original intake can be evaluated, as well as the ALI (Annual Limit of Intake), the DAC (Derived Air Concentration) [11].
We calculate the committed effective dose for a radionuclide
in the body with the ICRP mathematical tools and data from the
reference man. The committed effective dose is given for a period
τ= 50 years by the formula: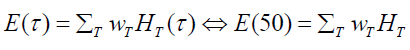 
(6)
where wT is the weighting factor for the tissue, and HT (τ) is the committed equivalent dose of tissue T given by equation (7)
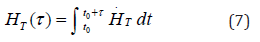
where τ= 50 years for occupational use, and τ= 70 years for the members of the public [12]. For a target organ T, we can calculate and sum the respective committed equivalent dose from all organs, known as source organ S.
where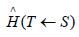 
is the equivalent dose in the target T(mean)
per disintegration of the radionuclide in S. US is the number of
disintegration of the nuclide in the source organ S for the 50 years
of the committed equivalent dose. The unique difference between
the dose calculated with ICRP II in one hand and ICRP 30 including
MIRD on the other hand, is that the committee of ICRP II used a
very simple phantom, the sphere ( all body organs and whole were
represented by spheres). The source and the target were the same.
Medical Internal Radiation Dosimetry (MIRD) System
The MIRD system has been extensively studied in class, so, here we are going write down the main equations that govern that system [13]. The absorbed dose in the MIRD system is given by the set of equations below:
This equation means that the Average or Mean Dose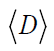 
is the
product of the cumulative activity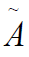 
by Mean Dose per activity S.
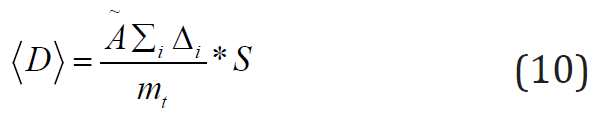
the average or mean dose is the ratio of the term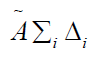 
by the
mass of target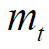 
[g].
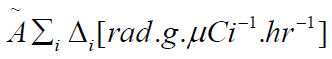is the product of the cumulative activity
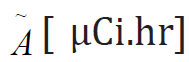by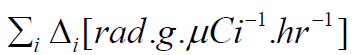 
, the sum of all the equilibrium
absorbed dose constants for all radiation emissions i.
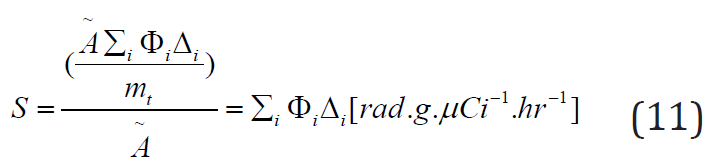
Equation (11) gives the Mean dose per cumulated activity,
where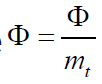 
is called specific absorbed fraction.
Radiation Dose Assessment Resource (RADAR)
The Radiation Dose Assessment Resource set up a website www.doseinfo-radar.com. The introduction of the internet gave the scientific community the impulse to disseminate a number of publications on data and procedures used in the system. The RADAR system is ruled by the equation [14].
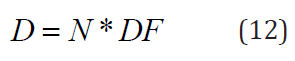
where and are respectively the number of transformations going on in the organ (the number of disintegrations is the area of the activity-time curve for a source region) and is given by the expression:
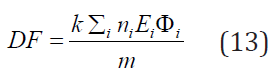
Mathematically speaking is similar to the mean dose per cumulated activity defined in the MIRD system by the equation (11) in 3.3 . The RADAR team put together collections of decay data, dose conversion factors, and classified, identical dose models for occupational workers and nuclear medicine patients. Furthermore, they developed a computer code, OLINDA/EXM that works with formulas (12), (13) and input data from RADAR site [15].
Specific Absorbed Fraction, Specific Effective Energy, and Committed Quantities
The specific equivalent dose in a target organ T caused by the
radiation emitted per disintegration by a radionuclide in source
organ S is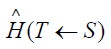 
. For a specific combination of the source organ
S , target organ T and the kind of radiation, we derive the value of 
from the fraction of the energy emitted in the organ S and absorbed
in organ T denoted , where R represents the type of radiation. The
specific absorbed fraction is the ratio of over the mass of the target
, is . Tables with value of the is the same as in equation (3) are
publishes by the ICRP. The values of for different type of radiations
are the same as in section 2 [11]. The Medical Internal Radiation
Dosimetry (MIRD) Committee have computed the absorbed
fraction for different organs and targets in the Reference Man
using Monte Carlo techniques based of the transport of photons
(monoenergetic and poly-energetic beam) through the human
body. Very often, a radiopharmaceutical in source organ S emits
several kind of radiation R, with a yield YR with a mean energy ER.
The product of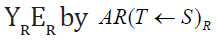 
gives the mean absorbed dose in
the target T per disintegration in source S by the type of radiation R.
The ICRP expresses the specific effective energy (SEE) transmitted
per gram of tissue in T from the emission of a specific radiation R in
the source organ S per disintegration as follows [12],
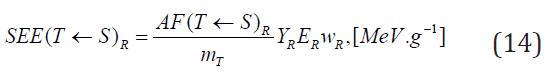
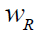is the weighting factor of radiation R emitted per
disintegration of a radionuclide in source S to the equivalent dose in
target T. To get this expression in radiation protection unit, we time
the SEE by the factor:
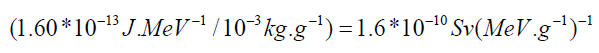
Performing the discrete sum for all kind of radiation emitted by the radiopharmaceutical gives a specific equivalent dose in target organ T, given below.
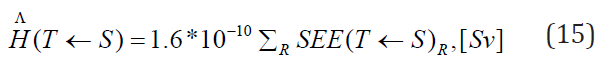
The committed equivalent dose is given by multiplying the number of disintegration US in 50 years by the specific equivalent dose above:
The committed effective dose obtained by multiplying the committed equivalent dose by the sum of all weighting factors for different tissues or organs:
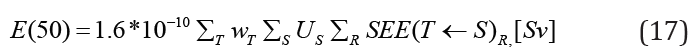
Suppose we have multiple radiopharmaceuticals in the body, therefore, to get the total committed effective dose, we add the individual contributions [12],
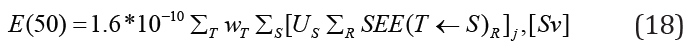
Conclusion
It has been long journey exploring, learning about the various internal dosimetry systems that are used to monitor, evaluate exposure for occupational workers as well as the public. All these dosimetry systems are crucial for protecting radiation workers and the public in order to prevent acute, rare effect of radiation, as well as minimizing the risk for long-term effects. Finally, we protect the people, also, by verifying adequacy at workplace controls and demonstrating regulatory compliance.
References
- IRCP (1979) Limits for Intakes of Radionuclides by Workers. Annals of the ICRP 2: 3-4.
- Mountford PJ (1996) Internal dosimetry: developments and limitations. European Journal of Nuclear Medicine 23: 491-493.
- Lehnert W, Schmidt K, Kimiaei S, Bronzel M, Kluge A (2016) Comparative Investigation of Internal Dosimetry Methodologies. Journal of Nuclear Medicine 57(2): 307.
- Sgouros G (2005) Dosimetry of Internal Emitters. Journal of Nuclear Medicine January 46(1): 18-27.
- Michael G Stabin (2007) Radiation Protection and Dosimetry: An Introduction to Health Physics. In Michael G Stabin(Eds.) Springer, New York, USA.
- Saha GB (2006) Physics and Radiobiology of Nuclear Medicine. In Saha GB (eds.) 3rd (edn.) Springer, New York, USA.
- Marinelli L, Quimby E, Hine G (1948) Dosage determination with radioactive isotopes II, practical considerations in therapy and protection. Am J Roent Radium Ther 59(2): 260-281.
- Quimby E, Feitelberg S (1963) (2nd). Radioactive isotopes in medicine and biology. In Quimby E, Feitelberg S (eds.) Philadelphia, Lea and Febiger, Washington Square, USA.
- Hine G, Brownell G (1956) Radiation dosimetry. In Hine G, Brownell G (eds.) Academic Press, New York, USA.
- ICRP (1960) Report of committee II on permissible dose for internal radiation.
- James E Turner (2007) Atoms Radiation and Radiation Protection. In James E Turner (eds.) Wiley, New York, USA.
- Health Physics Society (2004) Radiation Risk in Perspective. Position Statement of the Health Physics Society, Mc Lean, Virginia.
- Loevinger R, Budinger T, Watson E (1988) MIRD Primer for Absorbed Dose Calculations. Society of Nuclear Medicine .
- Stabin MG, Siegel JA (2003) Physical Models and Dose Factors for Use in Internal Dose Assessment. Health Physics 85(3): 294-310.
- doseinfo-radar.com
