OpinionIntroduction
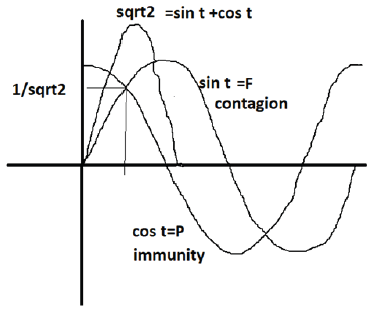
In this paper, we consider the famous double slit experience in light of AT Math. We see that familiar values for certain variables reoccur. This model can be used on problems such as virus transmission. We begin with the familiar sine equals cosine (Figure 1).
Figure 1: Immunity and Contagion.
Sine = cosine
Immunity =Contagion
cos θ = sin θ
Mv=1/t
Ln t(1/√2)=1/t
(1/√2)Ln t=1/t
(1/√2)y=y’
√2y=y’
∫√2y=∫y
(√2)y²/2=y
1/√2 ×y=1
y=√2
sin θ + cos θ
=sin 45 +cos 45=
=(1/√2)+(1/√2)
=2/√2
E = √ 2 =max of sin + cos (Figure 2)
Figure 2: Double Slit Experiment.
E = hυ
=6.626 x 1/π
=208.82
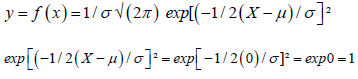
y=f(x)=1/σ√(2π) [1]
E=y=2.08816(√(2π)=1/σ
σ=.191
Entropy
S =1/ 2(Ln [2π eσ ²]
=-0.2366
t²-t-1=S=-0.2366
t²-t-1.2366=0
t=1.719 ; 0.719
E=0.582; 1.39
M=Ln t
=Ln 1.719
=542
M=Ln 0.719
=330
TE = M [0.15915] = 542(1/ 2π ) = 0.863 ~ 1/ sin 60°
TE=330[1/2π]=52.52
-1/2[X-μ)/σ]²=1
[(X-μ)(0.191)]²=-2
(X-μ)²=-0.7296
(X-1/2)²=-0.73
X²-X+1/4=-0.73
X²-X-1=0
GMP
V=iR
105i(1)
i=t²
√105=t
t=10.247
X²-X-1=0
10247²-10247-1=9397~940
f (x) =1/ (0.191)√ (2π )exp (940 − 0.5) / 0.191 ²
=[1/0.191√2] ×(201.7)
=0.7467~3/4=1/s
s=t
E=3/4 =1/s=1/t (Figure 3)
Figure 3: Double Split Experiment.
Note: https://brilliant.org/wiki/double-slit-experiment/
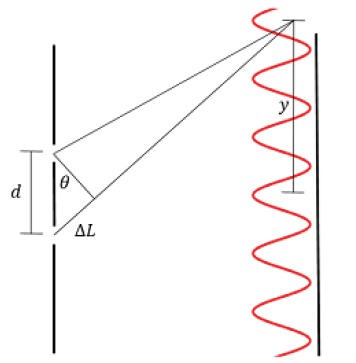
ΔL = d sin θ
ΔL=(1.042-2.556)=1.514
1.514=√2 sin θ
sin θ=-1.514/√2
=-1.07056
θ=-0.618
dsin θ = nλ
(√2)(-.107056)=11.3 λ
λ=1.339=1/E=t
t²-t-1=E
E=546
GMP E=-1.247
dθ=y
y=θ=-.0.618
nλ=dy/D
11.3λ=(1/√2)(-1.0786)/ (1)
λ=1.047~105=V+
λ=h/P̅
104.7=6.626/P̅
P̅=158.~π/2=cos θ
θ=809=1/c4
y=nλD/d
1=11.3(λ)(1)/(√2)
λ=8
1/λ=1.25=Emin
