Short CommunicationAbstract
In this short communication, the class of Zeid-G statistical distributions are introduced. A sub-model of this family is shown to be practically significant in fitting real-life data as well as simulated data. The researchers are asked to further develop the properties and applications of this new class.
Keywords: 1ΣαPT-Gfamilyofdistributions, Chen-G, Carbon Fibers Data
Introduction to the New Family
Firstly, we recall the following
Definition 1.1: [1] Let
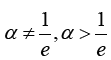
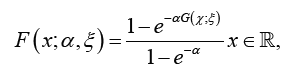
where the baseline distribution has CDF G(x;ξ ).
Proposition 1.2: [1] The PDF of the (1/e)a power transform family distribution is given by
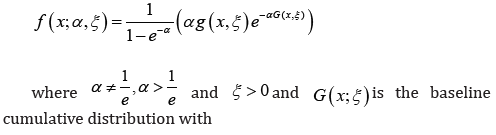
probability density function g (x;ξ )
Remark 1.3: The parameter space for α have been relaxed to α ∈R,α ≠ 0. The relaxation has been employed in several papers, and for example, see [2]
Using this relaxation, we introduce the following, inspired by the structure of the Chen-G CDF [ 3]
Definition 1.4: A random variable Y wil bel called a Zeid random variable, if the CDF is given by Zeid-G, that is,
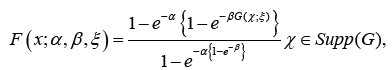
Where the baseline distribution has CDF G(x;ξ ),ξ is a vector of parameters in the baseline CDF whose support depends on the chosen baseline CDF. α ,β ∈R, and α ,β ≠ 0
Practical Illustration
Assume the baseline distribution is Normal with the following CDF
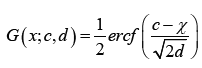
where x,c∈ℝ, d > 0, and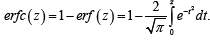 
. It follows from the Definition immediately above that we have the
following
Proposition 2.1: The CDF of Zeid-Normal, for x∈ℝ, is given by
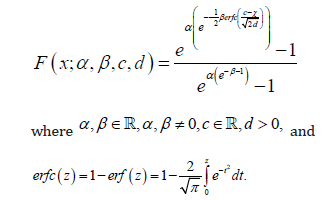
Remark 2.2: We write J ∼ ZN (α ,β ,c,d ), if J is a Zeid
random variable with the above
CDF
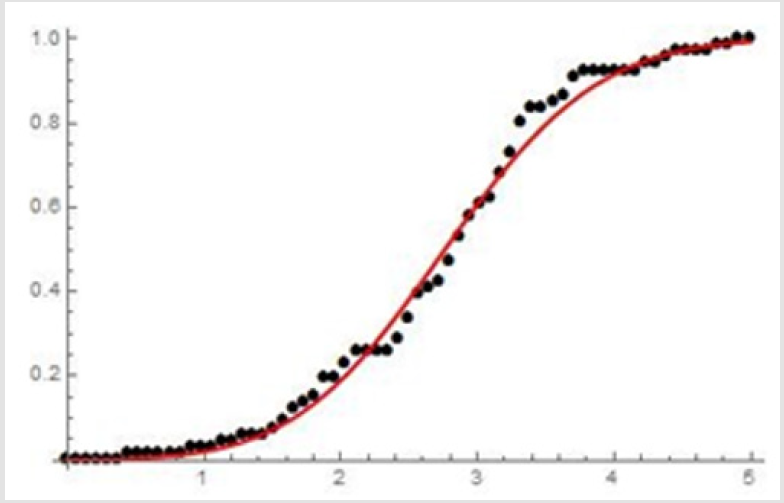
The new distribution is a good fit to real life data as well as
simulated data, as illustrated below [4] (Figures 1 & 2)
Figure 1: The cdf of ZN (1.6156, -0.474565, 2.89578, 0.897577) (red) fitted to the empirical distribution.
Figure 2: The pdf of ZN (-1.6156, -0.474565, 2.89578, 0.897577) (blue) fitted to the histogram of 10,000 random samples of ZN (-1.6156, -0.474565, 2.89578, 0.897577).
Concluding Remarks
In this paper, we introduced the Zeid-G family of distributions, and showed the Zeid-Normal distribution is a good fit to real life data as well as simulated data. We hope the researchers will further develop the properties and applications of the Zeid-G class of distributions.
References
- Anafo AY (2019) The New Alpha Power Transform: Properties and Ap- plications, Master of Science in Mathematical Sciences Essay, African Institute for Mathematical Sciences (Ghana).
- Ampadu CB (2019) A New T-X Family of Distributions, Annal Biostat & Biomed Appli 3(1).
- Lea Anzagra, Solomon Sarpong & Suleman Nasiru (2020) Chen-G class of distributions, Cogent Mathematics &Statistics.
- Alzaatreh A, Lee C, Famoye F (2014) T-normal family of distributions: A new approach to generalize the normal distribution. Journal of Statistical Distributionsand Applications 1: 16.
