Abstract
Protein 3-D structures are more functionally conserved than sequence and this claims the need of developing a computational tool for accurate protein structure comparison at the global and local levels. We have developed a novel geometry-based method for protein 3-D structure comparison using the concept of Triangular Spatial Relationship (TSR). Each protein is represented as a vector of integers, denoted as “keys”, where each integer represents a triangle formed by a triplet of Cα atom of the three amino acids in a given protein. Our method is independent of translation and rotation. The analysis of keys provides a deeper insight into structure and function relations of the proteins. We found two such keys: 3803315 (Ile-Leu-Leu) and 7903915 (Val-Ile- Leu). Nearly 100% of serine proteases, kinases, and phosphatases have one of these two keys, and these two keys have their specific Theta and MaxDist values. In addition, we observed shorter MaxDist found in the triangles from nonpolar amino acids (e.g. Val, Ile, Leu) compared with the triangle having charged amino acids (Arg, Lys, Glu, Asp). It is well known that hydrophobic amino acids are most likely found in the core of globular proteins. Because the core could play more important roles in protein folding than the protein surface, we suspect that the initial folding process, or some points during the folding of globular proteins could start from interaction between side chains of Val, Ile or Leu through hydrophobic interaction.
Keywords: Protein Similarity; 3-D Structure; Alignment; Comparison
Short Communication
The well accepted fact that protein structures are more conserved than sequences accelerates the discovery need to develop an accurate method to describe the 3-D relationships between proteins. Structural alignment or comparison captures information not detectable in a protein’s sequence due to the nature of protein folding: two amino acids that are far away from each other in a protein sequence may be brought close together in the 3-D structure when the protein folds. Challenges in quantifying structures have possibly resulted in the large number of approaches to this problem described in the literature. A number of algorithms have been developed and/or employed for structural comparisons: Maximal common subgraph detection [1], Ullmann subgraph isomorphism algorithm [2], and geometric hashing [3] in geometrybased; Monte Carlo [4], and Combinatorial Extension [5] algorithms in distance-based, and a genetic algorithm in secondary structurebased [6] comparisons. Dynamic programming algorithms have been used in both distance- [7-9] and secondary structure-based [8,10] comparisons. There are limitations in all existing methods. It requires efforts to develop better structural comparison methods. We have developed a completely different method in which each protein is represented by a vector of non-negative integers.
Methods
The detailed explanation for calculating “keys” will be reported in somewhere else. We observed from literature that all keys are not equal interesting, keys having MaxDist less than or equal to a certain distance might be interesting. Therefore, we started to filter keys by Maxdist less than or equal to 18 Å and then find common keys among proteins by performing a simple set overlap for the set of keys for each protein in a protein class. We started the experiment with kinase though any class can be picked first. We found too many keys with MaxDist less than or equal to 18 Å filter, therefore, we started to reduce the filter condition from MaxDist less than 18 Å in steps of one. We repeated the process and stopped at the filter condition MaxDist less than or equal to 11 Å as we found two useful keys 3803315 and 7903915 in kinases. Then we searched these two keys in two ways:
- Each key separately and took an average and
- Together in all proteins in each of kinase, phosphatases and serine protease classes.
Algo_common_key_search{
Input 1: A class of proteins, each protein in the format of a vector of integer ‘keys. Each protein will have a details file with 20 Columns as “Key AminoAcid0 SequenceId0 AminoAcid1 SequenceId1 AminoAcid2 SequenceId2 ThetaBin Theta MaxDistBin Maxdist x0 y0 z0 x1 y1 z1 x2 y2 z2”.
- Value of MaxDist as filter
Output: Common keys for a class of proteins
For MaxDist =18 to 6, in decreasing steps of 1:
#Step1: key filteration
For each protein in proteinList:
Filter keys by MaxDist
#Step2: Common key search
Initialize CommonKeyList = List of keys in the 1st protein in the protein list
Update proteinList = proteinList - 1st protein
For each protein in proteinList:
Common = Intersection of CommonKeyList and all keys of the protein
Update CommonKeyList = Common
If count of proteins in CommonKeyList <=5: #we are only interested into small amount of meaningful common keys
Break or end the algorithm
Analyze the keys in the common KeyList
} End of algorithm
Results and Discussion
Our Method is Independent of Translation and Rotation
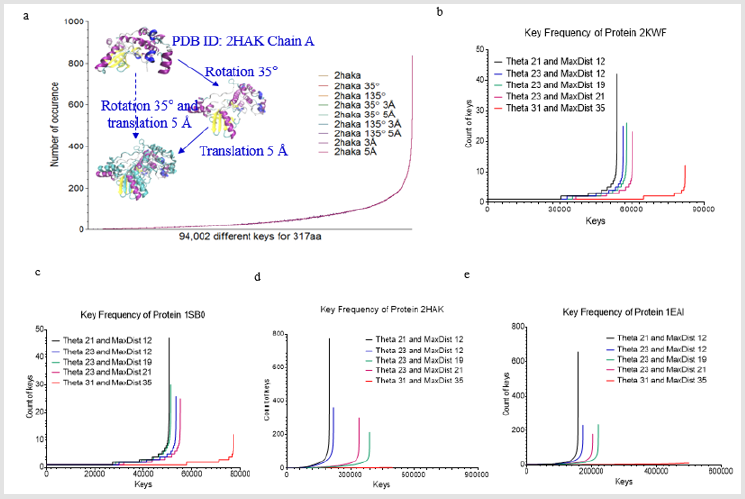
Figure 1: Key generation is independent of rotation and translation and increases in Theta and MaxDist bin numbers lead to a decrease in number of the keys with high frequency. (a one protein (PDB ID: 2HAK)) is randomly selected from PDB. 350 rotation and/or 5 Å translation were performed. Either rotation or translation yields the identical keys; b-e, Effect of Theta and MaxDist bin numbers on key frequency was analyzed in four proteins (b, PDB ID: 3KWF; c, PDB ID: 1SB0; d, PDB ID: 2HAK; e, PDB ID: 1EAI).
Before studying protein structural comparison, we want to examine whether our method is independent of translation or rotation. We chose one protein from PDB (PDB ID: 2HAK, Chain A) [11], rotated it 350 and/or translated it 5 Å, and the original structure along with all these transformations yielded identical keys (Figure 1a). This analysis indicates our method consider identical structures no matter how a structure is rotated or translated. Next, we investigated the effect of Theta and MaxDist bin numbers on key frequencies. We predicted that larger bin numbers have less possibility to generate the same keys for two triangles with similar geometries, but with a sufficient degree of difference in angle or length. As predicted, the number of keys with high occurrence frequencies decreases with increase in Theta or MaxDist bin number (Figures 1b-1e).
Identification of Common Keys for Proteins
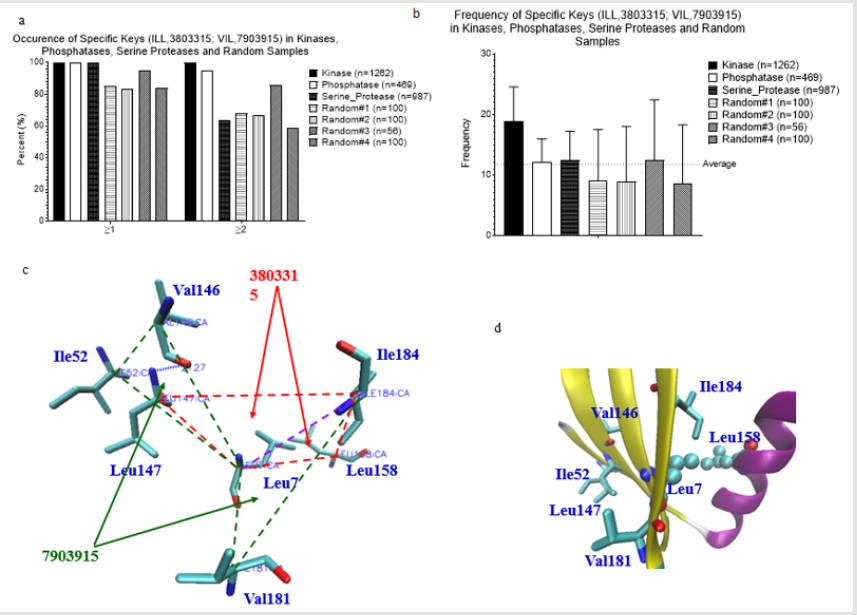
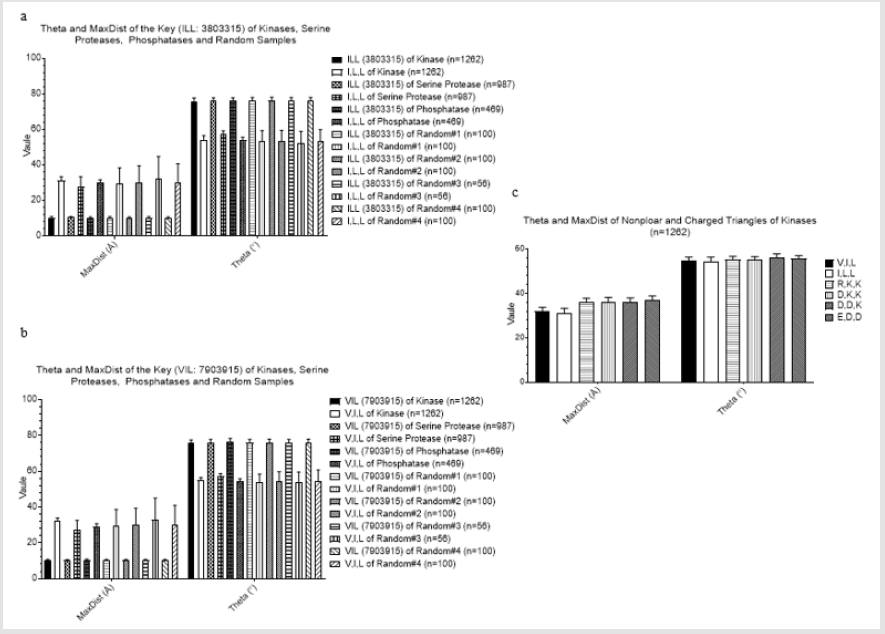
We were able to identify the Common keys from subclasses of serine protease, and subclasses of kinases and phosphatases. This motivated us to search for the common keys for serine proteases, kinases and phosphatases. We found two such keys: 3803315 (Ile-Leu-Leu) and 7903915 (Val-Ile-Leu). Nearly 100% of serine proteases, kinases, and phosphatases have one of these two keys (Figure 2a). Greater than 80% of four random samples have one of the two keys (Figure 2a). Average frequency of these two keys is between 11 and 12 (Figure 2b). A representative structure of the two 3803315 and two 7903915 formed by 7 amino acids is shown in Figure 2c. Six out of seven amino acids are located in a β pleated sheet and the remaining one is from an α helix (Figure 2d). We do not know the function of these two keys in protein folding. However, our analysis shows that 3803315 and 7903915 have their specific Theta and MaxDist values (Figures 3a & 3b). Hydrophobic amino acids are most likely found in the core of globular proteins. One supportive evidence is from the observation of shorter MaxDist found in the triangles from nonpolar amino acids (e.g. Val, Ile, Leu) compared with the triangle having charged amino acids (Arg, Lys, Glu, Asp) (Figure 3c). Because the core could play more important roles in protein folding than the protein surface, we suspect that the initial folding process, or some points during the folding of globular proteins could start from interaction between side chains of Val, Ile or Leu through hydrophobic interaction.
Figure 2: Frequency, and structure of two universal keys. a, Percent occurrence of two universal keys: 3803315 (ILL) and 7903915 (VIL) of the kinases, phosphatases, serine proteases and random samples was calculated; b, Frequency of two universal keys: 3803315 (ILL) and 7903915 (VIL) of the kinases, phosphatases, serine proteases and random samples was calculated. a-b, Number of the proteins in each data set is indicated; c, A presentative structure for the keys: 3803315 (ILL) and 7903915 (VIL) of a protein (PDB ID: 1EBB) selected from a random sample is shown; d, The amino acids corresponding to the keys: 3803315 (ILL) and 7903915 (VIL) are from the secondary structures (PDB ID: 1EBB).
Figure 3: Properties of two universal keys: 3803315 (ILL) and 7903915 (VIL). a, Theta and MaxDist of the key: 3803315 (ILL) are compared with those of the keys formed from all combinations of Ile, Leu, and Leu; b, Theta and MaxDist of the key: 7903915 (VIL) are compared with those of the keys formed from all combinations of Val, Ile, and Leu; c, Theta and MaxDist from nonpolar and charged triangles of the kinases were calculated.
Acknowledgement
The authors thank the support from Louisiana Board of Regents (LEQSF(2015-18)-RD-B-06) to W. X. and V.R.. Majority of our calculations were executed at LONI. We appreciate LONI support team; especially, thanks to Yuwu Chen, and Feng Chen.
Conflict of Interest
The authors declare no conflict of interest.
References
- Bron C, Kerbosch J (1973) Algorithm 457: finding all cliques of an undirected graph. Commun ACM 16(9): 575-577.
- Ullmann JR (1976) An Algorithm for Subgraph Isomorphism. J ACM 23(1): 31-42.
- Nussinov R, Wolfson HJ (1991) Efficient detection of three-dimensional structural motifs in biological macromolecules by computer vision techniques. Proceedings of the National Academy of Sciences 88(23): 10495-10499.
- Holm L, Sander C (1993) Protein structure comparison by alignment of distance matrices. J Mol Biol 233(1): 123-138.
- Shindyalov IN, Bourne PE (1998) Protein structure alignment by incremental combinatorial extension (CE) of the optimal path. Protein Eng 11(9): 739-747.
- Szustakowski JD, Weng Z (2000) Protein structure alignment using a genetic algorithm. Proteins 38(4): 428-440.
- Blundell T, Carney D, Gardner S, Hayes F, Howlin B, et al. (1988) Knowledge-based protein modelling and design. European Journal of Biochemistry 172(3): 513-520.
- Taylor WR, Orengo CA (1989) Protein structure alignment. Journal of Molecular Biology 208(1): 1-22.
- Lackner P, Koppensteiner WA, Sippl MJ, Domingues FS (2000) ProSup: a refined tool for protein structure alignment. Protein Eng 13(11): 745-752.
- Yang AS, Honig B (2000) An integrated approach to the analysis and modeling of protein sequences and structures. I. Protein structural alignment and a quantitative measure for protein structural distance. J Mol Biol 301(3): 665-678.
- Marx A, Nugoor C, Müller J, Panneerselvam S, Timm T, et al. (2006) Structural Variations in the Catalytic and Ubiquitin-associated Domains of Microtubule-associated Protein/Microtubule Affinity Regulating Kinase (MARK) 1 and MARK2. Journal of Biological Chemistry 281(37): 27586-27599.

 Short Communication
Short Communication