Introduction

The walking model of an anthropomorphic mechanism with absolutely rigid links has been considered in the researches on human movement mechanics [1] and in other researches carried out by the author. The calculations revealed that putting a leg on a surface originates a huge jolting acceleration [1,2]. This is why the link model minimizing the impact loads on the human musculoskeletal system is required. Every step on a hard surface results in an impact load on a foot of 18-20g of acceleration. Much of this acceleration is damped due to the foot construction. Approximately 6-7g is passed to the shin [3]. The forces arising in the absolutely rigid model stepping on a surface would have led to destruction of the human endoskeleton [2]. Almost entire energy of the impact due to the putting leg on a surface is dissipated in the lower limb [4]. In this research the limb is considered macroscopically. Let’s assume that the entire rod simulating the link undergoes deformation, whereas the joint does not [5]. We propose the model of the rod with variable length. The longitudinal forces applied along the rod and torques applied to joints allow the model movement [2,6-8].

Variable Length Link Definition

Let’s define the link of variable length from the point of view of theoretical mechanics. Our definition should be applicable to rodsystem simulation of human musculoskeletal system, exoskeleton and anthropo-morphic robot. The link of variable length is understood as a part of a mechanism between hinge joints. This part is a straight, may be fairly complex controlled structure that can change its length along the line between hinge joints, i.e. it can perform extension-contraction, but it is not prone to bending and torsion. At the same time, it constitutes a unified dynamic system within the mechanism. In fact, the skeleton elements are not straight, - they are crooked. The bone cross-sections are varying. Moreover, the inner part of the bones has complex multi-layer structure. For simulation purposes we will isolate the middle line of each bone and consider an exoskeleton as a structure consisting of straight rods that can change its lengths over time. We will replace joint with a hinge to which a required control-ling torque can be applied. The speed of disturbances arising in a model with absolutely rigid links is infinite. This is why the impact loads occurring when a human walk would have spread over all organs, including the brain, instantly [2]. In reality, this does not happen. Hence, the approach to simulation of the human walk based on absolutely rigid models is not adequate [2]. Therefore, we should consider an organism as a deformable system. The deformity, i.e. the links variability of the human musculoskeletal system during walking process should be considered [6-8].

Reasons for Changing Link Length

When simulating the human musculoskeletal system, the change of the link length can be related to a number of factors:

a) The forces and reactions arising during walking, and causing deformation of bones, and cartilaginous tissues of joint [4,5]

b) Displacements in the joint caused by synovial fluid and imperfection of the joint form

c) The link length change caused by the fact that the bone is not a perfectly straight rod

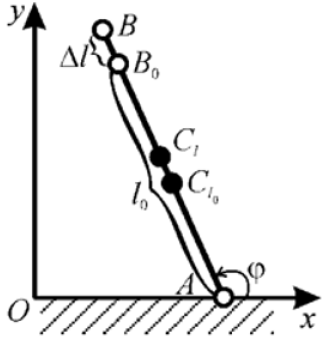
d) When the head of the bone rolls over the meniscus in the knee joint, the link length varies because the position of the rotation axis changes (Figure 1) [9].

Figure 1: The trajectory of the instantaneous rotation centres (marked with points) in a healthy human knee [9].

In the research [10] it is pointed out that failure to account for the bone rolling over the meniscus in the knee joint, and consequently for the link change results in injury of the person using an exoskeleton with an absolutely rigid links. In the same paper, an equivalent kinematic model based on irregular shaped cams simulating bone-to-bone contact in the human knee joint was proposed. The shape of the cams was obtained by identifying the instantaneous rotation center. The video observation used as the basic measurement instrument allowed obtaining the information about the instantaneous rotation center movement in the knee joint. Therefore, the length variation of the link is related not only to the forces and torques applied to it during movement, but also to the limb geometry. The limb length depends on the relative position of the human musculoskeletal system links. In order to effectively describe the link length variation in response to various factors we should consider the model of the link with a variable length as a function of time. All parameters, such as angle of rotation, length, the position of the mass center of the link, are the functions of the time:

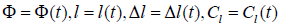
Description of Variable Link Model

As such a model, let’s consider the model of the link with variable length. Consider a rod with variable length shown in the figure 2, where Φ - the angle of the rod rotation, С_l0 – the initial position of the rod mass center, С_l – the current position of the rod mass center, l₀ – the initial length of non-loaded rod, l – the current length of the rod during motion. The rod length change can be described as:

Figure 2: Variation of the rod length in the process of its motion.

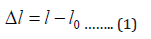
If Δl < 0, the rod is contracted, if Δl > 0, the rod is extended. The torque M(t) is applied at the hinge A. The torque M(t) controls the model and defines the rotational movement of the rod. The movement of a multi-link mechanism is considered as a dynamics problem of a mechanical system. It is described with differential equations of the system motion in the form of Lagrange equations of the second kind for rods with variable length. The variation of parameters during walking is considered as a problem of parametrical identification [11] (Figure 2).

Generally, the problem of parametrical identification is solved with the state space expansion method. In the considered case of n-link mechanism we will assume that the rod lengths li(t) (i = 1, …, n) are additional degrees of freedom, i.e. generalized coordinates. The link length l varies as a result of applied forces along the rod which either extend or contract it. We assume that l(t) = l0 + Dl(t). The variation of the link length can be implemented in an exoskeleton model in a variety of ways. The link length variation can be given, or it can be derived from the system of differential equations of motion, if the longitudinal controlling force is specified.

Conclusion

Active controlling torques can be implemented as electric motors with sensors of rotation angle, angular velocity, and feedback control unit. Active torques apply the required brakes when a leg is placed on the surface, and also create an acceleration when the leg pushes off the surface. The energy recuperation and hence the energy saving is possible when the breaks are applied during exoskeleton motion. The problem of high energy consumption when driving an exoskeleton or an anthropomorphic robot is still urgent.

Acknowledgment

The reported study was funded by RFBR and Smolensk region, project number 19-48-670002.

References

1. Zatsiorskiy VM, Aruin AS, Seluyanov VN (1981) Biome-chanics of the human motor system. Moscow, Fizkultura I sport pp. 143.
2. Chigarev AV, Borisov AV (2011) Simulation of controlled motion of the bipedal anthropomorphic mechanism. Russian Journal of Biomechanics 151(51): 69-83.
3. http://www.it-med.ru/library/p/ploskostopie.htm.
4. Chigarev AV, Borisov AV (2009) Mathematical model of distribution of the impact impulse in the lower finiteness of a person with a leg on bearing with allowance for element deformability. 16^th INTERNATIONAL CONGRESS ON SOUND AND VIBRATION 2009, ICSV 2009 Krakow, Russia, pp. 3856-3858.
5. Borisov AV (2010) Elastic analysis of multilayered thick-walled spheres under external load. Mechanika. Kaunas University of Technology 84(4): 28-32.
6. Borisov AV, Rozenblat GM (2018) Modeling the Dynamics of an Exoskeleton with Control Torques in the Joints and a Variable Length of the Links Using the Recurrent Method for Constructing Differential Equations of Motion. Journal of Computer and Systems Sciences International 57(2): 319-347.
7. Borisov AV, Rozenblat GM (2017) Matrix method of constructing the differential equations of motion of an ex-oskeleton and its control. Journal of Applied Mathe-matics and Mechanics 81 (5): 351-359.
8. Borisov AV, Konchina LV, Chigarev AV (2015) Twelve-Link Exoskeleton with Biological Endoskeleton Properties. Journal of Machinery Manufacturing and Automation 4(3): 23-37.
9. (2001) Basic biomechanics of the musculoskeletal system. In Margareta Nordin, Victor H Frankel (Eds.). (3^rd ), Lippincott Williams Wilkins 2001 - 467.
10. Piña Martínez E (2015) Inverse Modeling of Human Knee Joint Based on Geometry and Vision Systems for Exoskeleton Applications / Eduardo Piña-Martínez, Ernesto Rodriguez Leal. Mathematical Problems in Engineering 2015: 145734.
11. (1987) Reference book on automatic control theory. In AA Krasovskiy (Eds.), Moscow, Nauka.

Abstract

The walking model of an anthropomorphic mechanism with absolutely rigid links has been considered in the researches on human movement mechanics [1] and in other researches carried out by the author. The calculations revealed that putting a leg on a surface originates a huge jolting acceleration [1,2]. This is why the link model minimizing the impact loads on the human musculoskeletal system is required. Every step on a hard surface results in an impact load on a foot of 18-20g of acceleration. Much of this acceleration is damped due to the foot construction. Approximately 6-7g is passed to the shin [3]. The forces arising in the absolutely rigid model stepping on a surface would have led to destruction of the human endoskeleton [2]. Almost entire energy of the impact due to the putting leg on a surface is dissipated in the lower limb [4].