Abstract
Mini Review
Some pretty simple forms of mathematical relations, which could be suitable for assessment of concentration of different kind of medications that are contained in patient’s blood and tissue during medical therapy are considered.
1) The current pharmaceutical industry makes pharmaceutical products more ideal. And their usage must be strictly controlled in dosage and in real concentration in patient’s blood and tissue as well. Undoubtedly such control is needed for changing the strategy of the patient treatment on the one hand, and on the other hand it is needed for ensuring the safety of the therapy, anesthesia, assessing the intoxication level and in some other possible cases. In this regard, first of all, we should pay attention to the fact that the total relative amount of the active drug, as a rule, is extremely low, which allows to use linear forms of mathematical relations. For this reason, we restrict ourselves to the first two terms of the expansion of the multiple-integral Volterra series [1]
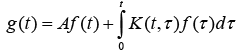
where t is time, A= const, K(t,τ ) is the kernel of the integral operator. Also we should note, that medicine remedies may act with a delay regarding the time of its reception. And once inserted may have an effect on the patient for a long period of time. And therefore, the relationships of hereditary type [1] should be used for the specified purposes.
2) Let us assume that a certain medicinal substance is injected into the patient’s blood; its concentration, calculated by taking into account the patient’s body weight or blood volume or in some other way, is denoted by q(t). The general form of the linear relationship of the hereditary type, which determines the current value of the concentration of the drug in the patient’s blood r(t), will be written as a linear functional
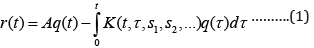
where s1, s2……- a set of parameters necessary to clarify the treatment process. Here and further, all processes will be considered starting from the moment t=0, which is why the lower limits of integration in all cases will be considered equal to zero. In the simplest case, under constant conditions of use of the medicinal substance, provided that the process under study is invariant with respect to the start of time, the relation (1) can berepresented as the Boltzmann – Volterra relation [2]:
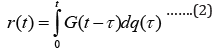
To apply the relation (2), it is necessary to define the function G(t) . This can be done most simply by using the Heaviside function
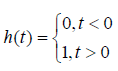
Then for q(t) = q0h(t) the relation (2), by virtue of the fact, that dq(t) = q0h(t), where δ (t) is the Dirac delta function, will take the form r(t) = G(t)q0 from where we find
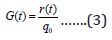
In this case we assume r(0) = q0 and then A=G(0) =1 [2]. In our opinion, the function G(t) , which characterizes the rate of excretion of a certain drug from the body, can be used for its functional diagnosis. Of particular practical interest is the use of the ratio (2) to calculate the concentration of the drug in the patient’s body when it is instant introduction, in particular, by intravenous injection, as well as in the case of its introduction by means of a dropper, produced at a speed q(t)=at . In last case the ratio (2) is reduced to the form:
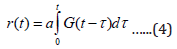
Let us consider the procedure for applying the relations (2) and (4). Let us assume that we have made the necessary measurements of the concentration r(t) of a drug administered by intravenous injection. We will consider this process is fast enough and therefore use the Heaviside function to describe it: q(t) = q0 h(t) . Using the results of these measurements, we define the function G(t) by means of the relationship (3). It can be seen that the application of the relation (2) in the general case or the ratio (4) – in this particular case, does not lead to any difficulties.
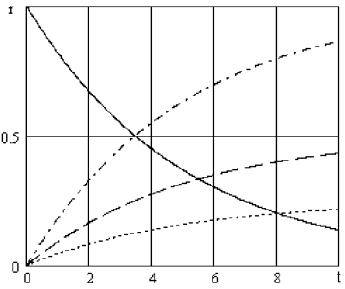
Let’s consider an example of application of these relations. Let us assume that the influence function G(t) has the form G(t) = e−0.2t . In this case r(t) = q0 e− 0.2t . Thus, the curve of the dependence of the current value of the drug concentration r(t) on the time t after the intravenous injection for the case q0 =1 is represented by a solid line on the Figure 1. The same Figure 1 shows the dependences of the drug concentration determined by the ratio (4) in the specified period of time (0 ≤t ≤ 10) during the drip administration of the drug. They are represented by the dotted line when the drug is administered for the law q(t)=0.05t ; by the dashed line when the drug is administered for the law q(t) = 0.1t , and by the dash-dotted line when the drug is administered for the law q(t) = 0.2t . Let us also note that in the absence of taking into account the decreasing of the drug, provided by the mathematical model, the total amount of the drug administered over the specified period of time, in the first case would be equal to 0.5, in the second case 1.0 and in the third case -2.0 (Figure 1).
3) The process of oral administration of medicines has a slightly different character from the point of view of applying the mathematical model under consideration. Here, as above, there are many accompanying factors that significantly affect this process. We will not specify them, but only pay attention to the possible importance of taking them into account. For example, the concentration of the drug in the stomach will decrease if the amount of liquid in the stomach increases, and this fact should be reflected in the calculations using the ratios given here. The general form of the linear ratio of the hereditary type, which determines the current value of the concentration of the drug that eventually enters the patient’s blood when taking the drug orally, will be recorded using the functional dependence
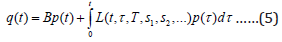
The symbols s1, s2…. have the same meaning as above. Assuming that the relation (5) is applied under constant meanings of the parameters s1, s2…. if it is invariant with respect to the time reference, we bring it to the form of the Boltzmann-Volterra relation:
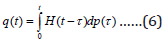
The introduced here influence function H(t) is also a functional characteristic of the body that determines the amount entering in the bloodstream of the orally administered drug. The simplest way to determine the function H(t) is to set a constant value of the drug concentration using the Heaviside function: p(t) = p1 h(t) . In this case, using the measured drug concentration in the body, we have
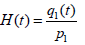
At the same time, we assume B= H(0), and the value q1(0) is equal to the value of the concentration of the drug immediately after its administration, at the time t=0+. After determining the function H(t), the use of ratio (6) to determine the concentration of the orally administered medication in the patient’s body does not present any difficulties. Note also that experimentally defined functions G(t) and H(t) can be replaced with analytical approximations, which significantly facilitates the use of various types of mathematical packages of personal computers when calculating the current values of the concentration of drugs in the body.
4) The history of the use of hereditary forms of defining relationships, including those given above, is quite short. This theory is most well developed in relation to technical applications. It should be noted, however, that in addition to the linear theory of hereditary relations, theories that take into account the violation of linearity and analyticity – factors that reflect the limitations of the used linear forms of relationships have recently received rapid development. In technical applications limit parameters – the linearity limit and the analyticity limit are usually introduced. Such parameters are introduced, for example, in the simplest nonlinear hereditary piecewise linear form [3, 4]:
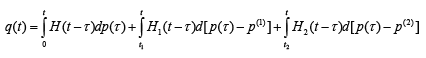
where values p(1) and p(2) in relation to the medical and biological aspects of the problem, it would be appropriate to call, despite the universality of the terms linearity and analyticity, the level of criticality and the level of fatality,t1 and t2 -the moments of time at which these levels of drug concentration are reached.
Acknowledgement
None.
Conflict of Interest
No conflict of interest.
References
- Volterra V (1959) Theory of functional and of integral and integro-differential equations. Dover Publication, Inc, New York, USA.
- Ilyushin АA (1970) Pobedrya B.E. The basis of mathematical thermo-viscoelasticity theory. Science, (in Russian) Мoscow, Russia.
- Sharafutdinov GZ (1985) On the one form of constitutive relations of the viscoplasticity. Problems of strength 9: pp. 97-102.
- Sharafutdinov GZ (2019) Application of piecewise analytical and piecewise linear forms of constitutive relations of hereditary type in the study of metal creep. Proceedings of the Russian Academy of Sciences. Solid mechanics 4: pp. 27-38.

 Mini Review
Mini Review