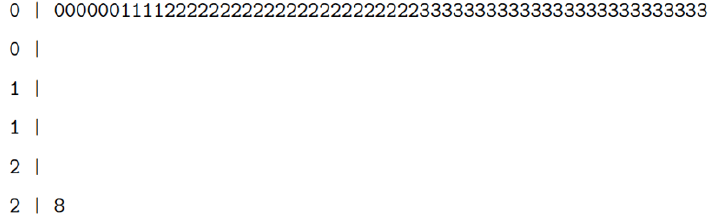Abstract
A considerable amount of attention has recently been focused on addressing issues related to data fraud. As this specific example shows, statistical analysis can be used to determine when data fabrication, falsification or plagiarism has occurred. Presented here is an example of statistical data analysis showing how the original data (HI data) set, reported as being fabricated, was in fact statistically shown to be valid/real data; while another set of data (Hansen data) was reported as fabricated and was statistically shown to be falsified and plagiarized from the original HI data. This particular case looked at changes in weight related to a diet study – with implications for its impact on heart disease and cancer – as evidenced by the involvement of Revival Soy and Avon. This paper should be used not only for scientific publication analysis of data fraud with particular emphasis in Cardiology and Oncology but should also set the irrefutable standard for data fraud analysis and interpretation in and by all U.S. and International Courts.
Keywords: Data Fabrication; Data Falsification; Data Plagiarism; Statistical Analysis of Data Fraud; ORI; Dr. Alicia Carriquiry; Dr. Mark Kaiser; Iowa State University; Dr. Gordon Harrington; DHHS; FDA
Introduction
In recent years a considerable amount of interest has been generated in determining if published data is valid or has been fabricated. Multiple social media sites, many of which are discussed on twitter now question research being published from multiple individuals and institutions around the world. The motives for questioning published data include
a) Disagreement with published findings generated by individuals with dichotomous positions (e.g. classically diet studies).
b) The potential for actual data fabrication, falsification and plagiarism, and
c) A break down in social structure itself where individuals now feel free to anonymously attack with impunity published studies for a variety of reasons; some valid, some not (Flow Chart 1).
The process whereby individuals are selected as reviewers for scientific journals begins with the fundamental training of a researcher under the tutorage of a senior scientist in a given field (e.g. Medicine). Over time the scientist-in-training has the opportunity to become part of the team of publishing scientists, which includes the opportunity to present abstracts at scientific conferences and eventually to be included on published papers submitted to journals. With sufficient publications and research experience, the scientist-in-training usually accomplishes advanced degrees and becomes recognized in the literature as having an area(s) of expertise.
Once recognized with sufficient publications (abstracts and papers), applicable journals will submit a request for the scientist to become a reviewer for submitted journal papers and will ask the scientist to review papers to determine if the submitted papers should or should not be published. While the scientist now serves as a reviewer, they are expected to objectively and without prejudice review the manuscripts submitted to them by the journal editor. Once sufficient time and expertise in an area has been established, usually decades as a reviewer and published scientist, researchers may eventually be offered the opportunity to be a journal editor, whose responsibility it is to initially review submitted papers to determine if the submission should be considered for publication and reviewer consideration.
This established scientific approach has long been the standard in the scientific community with the expectation that once reviewed and published, refutation of a publication can be accomplished in the scientific literature through “letters-to-the-editor” and by the publication of data proposing alternative explanations, which are then “scientifically” discussed open and honestly, understanding that as science evolves, there will be honest disagreements as we struggle to find the truth. This paper focuses on the scientific process of establishing the second issue; one of data fraud either through fabrication, falsification or plagiarism, using a case example showing how statistical analysis found an unexpected source of data fraud.
Statistical Methods for Establishing Data Fraud
The Institute (HI) conducted a study designed by a snack food manufacturer. The study was a rather simplistic study, asking 60-people to substitute the snack food for any in between meal snacks. Analysis of the results were statistically evaluated using specialized statistical programs developed at a Major University in the Department of Statistics, by Drs. K and C following questions regarding data fabricated. Following failure by Drs. K and C to find any evidence of data fabrication, using specifically developed statistical programs developed more than 5-years after the research had been completed, programs which were developed to specifically prove data fabrication (beginning with the premise that there had been data fabrication) as described in this paper; Drs. K and C concluded there was no data fabrication but were unable to explain why the statistical tests they had developed to expose data fabrication were unable to show that the Hansen data was fabricated, when the Hansen data had been submitted to Drs. K and C under the premise that the Hansen data were entirely fabricated. In the second part of this paper following the discussion of the statistical methods used by Drs. K and C to look for data fabrication, we will look at the use of Shewhart charts and other statistical analysis of the data sets looking for data fabrication, falsification and plagiarism as conducted by Dr. H, a recognized Statistical expert at a second University.
Shewhart charts are used in the Industrial setting to assure consistency in production. Statistically speaking, Shewhart charts and analysis look for consistency; viz. in the instance of data fraud – Plagiarism. In an effort to avoid any change in the reports including typographical errors, and to use the language of the statisticians themselves, we now proceed reading the reports as generated first by Drs. K and C. and later by Dr. H. Any changes or redactions which would identify patients or institutions will be noted by bracketed ([]) changes for the purpose of reading ease and confidentiality and bold font for emphasis added with the exception of the title headings which were originally in bold font. We begin with Dr. K’s report of the Drs. K and C analysis and report. The Office of Research Integrity (ORI) confirmed Drs. K and C statistical report and methods as “standard for this type of analysis.” In the third and last part of this paper, we will simply show the tabulated data from both the HI and Hansen data in addition to three graphics showing weights at baseline (0-weeks), 2 and 4-weeks on the diet, allowing the reader to see how changes in the HI weights are mirrored (plagiarized) by the Hansen data set.
Part I: The Drs. K and C Report - as Written by Drs. K and C
Background
My understanding is that questions have been raised about the authenticity of the data produced by that study and, specifically, whether some of those data may have been fabricated. Statistical examination of a set of data cannot “prove” or “disprove” falsification of data records, but it can determine whether certain types of anomalies exist that would not be expected in data from most scientific studies. The goal of this exercise was to uncover any such anomalies that might exist in the data from this study. The data used in this analysis were taken from a final report signed by the principle investigator [] and provided to me via electronic transmission by [the HI]. The data contain records for 60 individuals that consist of values for height, initial weight, weight at two weeks, weight at four weeks, and body mass index at the same time points as weight. My examination of these data makes use of only the directly recorded variables of height and the three weight measurements. Also provided was a set of data I was told were entirely fabricated by a Mr. Hansen and these data are examined in the same manner as for the HI data.
Methods of Examination for Fabricated Data
Appropriate statistical methods for examination of data to detect potential fabrication depend on the characteristics of the study or studies of concern, including study design, objectives, and the analysis used to reach conclusions. Also important is the type of data fabrication suspected. The best methods for detection of one or a few fabricated data records differ from those more appropriate for the detection of wholesale fabrication of an entire or nearly an entire data set e.g., Buyse et al. [1]. The study of concern here was of a very simple design with apparently self-selected subjects and lacking multiple medical centers or treatment groups, precluding the use of comparison of multiple centers or a suspect data set to an unsuspicious one e.g., Al-Marzouki et al. [2]. The examination reported here focused on three aspects of the data records, marginal and joint data structure, recorded data values, and influence on results. The motivation for considering these aspects of the problem are described in this section.
Fabrication of data generally has a specific objective, either to influence the outcome of data analysis (e.g., show an effect of one or more treatments) or to avoid the effort needed to properly conduct data collection if a pattern seems clear from an analysis of some actual data. The former situation may result in alteration of one or more data records that have disproportionate influence on the outcome of statistical analysis for the study. Alternatively, if an entire data set is fabricated to exhibit an effect of some type (e.g., a difference in treatment group means), other characteristics of typical data sets that might also show such an effect (e.g., variance or covariance structure) are difficult to match. That is, most scientists cannot preserve higher-order structure in falsified data while achieving the desired first-order differences (Haldane 1948). The fabrication of data records as a matter of convenience may sometimes be detected based on either the number or distribution of digits in recorded data (e.g., Hill 2008), Walter et al. [3]. For example, the presence of “extra” digits in recorded data may indicate that other, possibly legitimate, records have been averaged to produce the falsified data, or a fabricated data set may contain a preference for certain digits in either the first or terminal places. This latter phenomenon is related to the fact that the human mind is a poor random number generator.
While a comparable data set from an undisputed study is not readily available for this analysis, it is possible to make use of theoretical probability distributions for comparison with the [HI] and Hansen data sets. Simulation of random values from theoretical probability distributions can be used to describe the expected behavior of actual data. Serious departures from such behavior are then a signal at something may be amiss in a given set of values. The [snack food] study resulted in a four-dimensional multivariate observation for each subject, height, weight 0, weight 1, and weight 2. Assuming (which can be reasonably verified for the [HI] data) that a multivariate normal distribution provides a good model for the marginal and joint data characteristics, simulated values from this distribution can be used to examine what might be expected in terms of recorded data values (e.g., terminal digits) and whether or not averaging results should appear in randomly generated data.
Marginal and Joint Data Structure
The first approach used in this exercise was to examine the marginal and joint data structures for the entire set of data. This examination might indicate the presence of records that were altered in a manner that failed to preserve the overall coherence (or general behavior) of the collection of data in a manner consistent with typical probabilistic rules. For example, if a number of records were falsified for a particular weight (e.g., weight2 at week 4) they might stand out as having a different relation with height than they did at an earlier stage (e.g., weight1 at week 2). If entire data records were falsified the relation among variables in those records (ht, wt0, wt1, wt2) may not follow the overall pattern of the set of data. In a sense, then, this examination is one of data consistency. An individual falsifying a few data records would need to take care that those records “fit” the general pattern in the entire data set. An individual falsifying the bulk of records or fabricating an entire data set would need to take care that those records were both biologically consistent and probabilistically consistent.
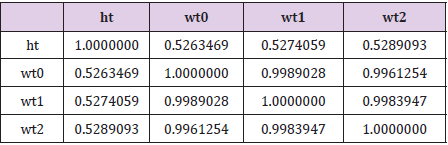
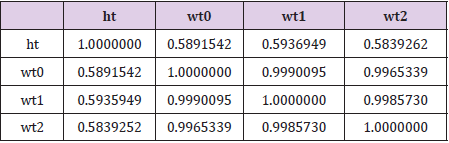
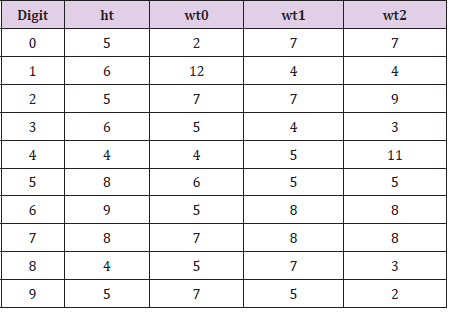
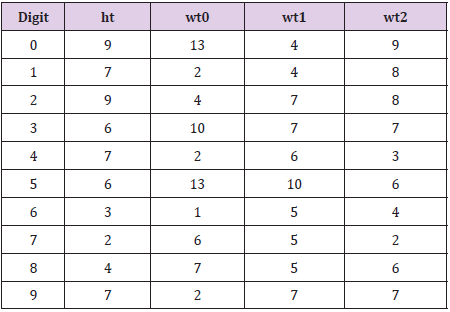
Probabilistically consistent here means that there should exist some joint probability distribution that could have “generated” the observed data. While no theoretical probability distribution is “correct” in a real problem, real data tend to follow the patterns of data simulated from theoretical distributions and dictated by the rules of probability. Falsified data often fail to exhibit this same consistency (unless, of course, they were produced via simulation from theoretical probability distributions). Basic summary statistics for the [HI] data set are presented in Table 1 and similar values for the Hansen data are presented in Table 2. The values in Tables 1 & 2 are quite similar. The greatest difference in summary statistics from these sets of values is that the range (maximum value minus minimum value) for weights in the Hansen data set are more constant than for the [HI] data set. These ranges are reported in Table 3. The greater consistency in range for the Hansen data may be indicative of a more systematic method of data production, but without the knowledge that these data are purportedly fabricated it would be difficult to reach that conclusion on the basis of the ranges given in Table 3.
Correlations among the variables of height, weight0, weight1 and weight2 are reported for the [HI] data in Table 4 and the Hansen data in Table 5. Again, these values are quite similar, actually remarkably so. There is little to suggest that either set of data are not internally consistent. Extremely high correlations (for which the values of correlations between weight0, weight1 and weight 2 would qualify) are sometimes taken as an indication of results “too good to be true” e.g., Akhtar-Danesh et al. [4]. But that is a weak argument against either the [HI] or Hansen data sets in this case. The reason is a combination of the ranges for weight measurements in Table 3 and the physiological realities of how much weight an individual can gain or lose in a period of several weeks. Correlation is a measure of linear association between two variables and this measure is affected by the range of values considered. A wide range of initial values (e.g., a range of 155 lbs. in weight0 for comparison with weight1 or a range of 156 lbs in weight1 for a comparison with weight2), coupled with the biological reality that any individual is unlikely to lose or gain more than a small fraction of their initial value relative to the initial range indicates that high correlations are to be expected in this situation. Both the [HI] and the Hansen data are also consistent with the anticipation that weights observed at more distant time points (i.e., weight0 and weight2) should be less highly correlated than weights observed at less distant time points (i.e., weight0 and weight1).
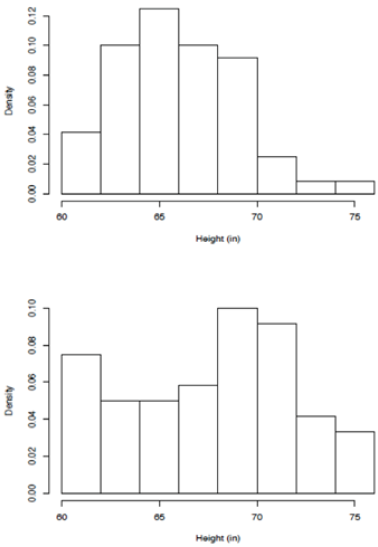
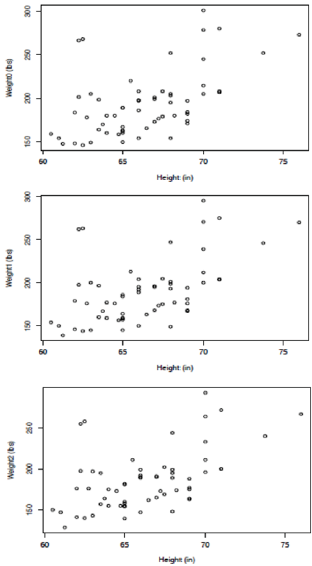
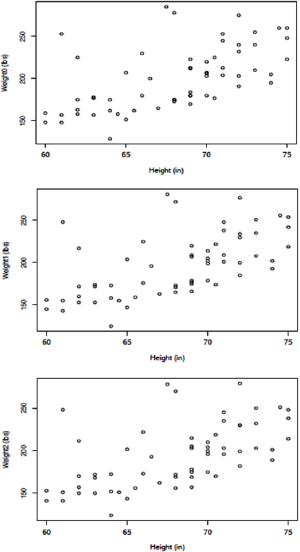
One caution is in order here concerning the marginal distributions of the variable’s height and initial weight (i.e., weight0). It may be tempting to compare the empirical distributions (as histograms, for example) of these variables in a given set of data to what is known about values for the national population as a whole. For example, if one looks at the distribution of weights for the population of males and females at large, one should anticipate seeing a bimodal distribution. In a study of 60 individuals chosen randomly from the overall population one might anticipate a similar distribution for observed values in the sample. However, in a set of 60 self-selected individuals, such as in the current situation, one may not [originally emphasized] anticipate that the empirical distribution of the sample will appear closely similar to the population distribution. The distribution of heights or initial weights in a self-selected sample from any population are just as likely to look dissimilar to the population distributions as they are to look similar to the population distributions. Histograms of height values for the [HI] and Hansen data are presented in Figure 1. Here, the distribution of heights from the Hansen data appears to have an excess of tall individuals, which would not be expected if the data corresponded to a random sample of the population of individuals in the United States. However, given that the values would not correspond to a random sample of individuals in the population, it would be misleading to claim that the empirical distribution in the lower panel of Figure 1 provides evidence of falsified data.
Scatterplots of weights at times 0, 1 and 2 against height are presented for the [HI] data in Figure 2 and for the Hansen data in Figure 3. The first thing to note here is the similarity of the three scatterplots for each set of data. This should be expected, again because of the total range of weights contained in the data sets and the physiological realities of how much weight can change for humans over a period of several weeks. It appears that one could pick out individuals on these plots and that is, in fact, true. What would be disturbing would be to find individuals with radically different positions on one or more of the three plots and that does not occur. One may also notice that there are more widely scattered points above the bulk of the data pattern than there are below, for both data sets. This is not necessarily to be unexpected, at least in the [HI] data, because the self-selected sample of participants were individuals who considered themselves overweight. Statistically, this data pattern suggests distributions of weight for given heights that are skew right rather than symmetric. That this same pattern is exhibited in the Hansen data suggests that the fabrication of the Hansen data set was undertaken in a way to preserve features of the [HI] data.
Overall, there is little in either of the sets of values examined to suggest that they could not be the result of studies with an absence of fabricated data. Both sets of values may be considered as internally consistent. At this point we would have no justification for suggesting that either set of data have been manipulated in a manner consistent with the falsification of data. Examination of data sets in the manner of this section is not a powerful approach for identification of anomalies for this situation because of the lack of a reference for comparison. The population as a whole will not serve this purpose because subjects in the [HI] study were not intended to be a random sample from the population, and we lack data from a comparable undisputed study for comparison as well. What we can say is that neither data set contains obvious glaring inconsistencies that would suggest fabrication of data.
Recorded Data Values
Any numerical data value consists of a sequence of digits. For example, the value of 156 for an initial weight in this study has the digits 1, 5 and 6, in that order. There are two common approaches for examination of recorded digits in data records – investigation of recorded values that contain “extra digits”, and comparison of distributions of the values 0 through 9 in various places in the data (e.g., first digit or last digit). We consider these two approaches in turn.
Records with Extra Digits
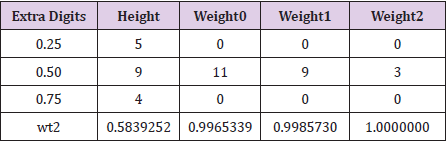
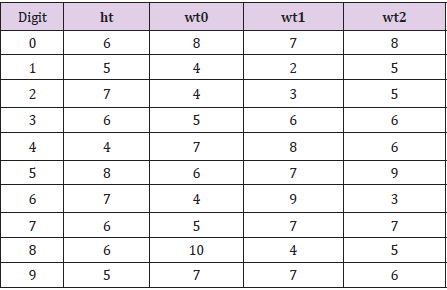
The majority of the data contained in the [HI] data set are recorded to the nearest whole number (e.g., height to the nearest inch, weight to the nearest pound) but there are a number of records that contain extra digits of either 0.25, 0.5 or 0.75. Table 6 presents the frequencies of these extra digits for the four observed variables. Data records with extra digits relative may indicate that other data records were averaged to produce the suspect record e.g., Walter et al. [3]. For example, if two records with weights of 174 and 177 are averaged the result is 175.5, and the extra digit is easily recorded by an individual falsifying data. Of course, the mere presence of extra digits in some records does not necessarily indicate the record was constructed, but in the absence of falsification it would be unusual for one (entire) record to be the average of two others, even more unusual for this to be true of two records, and so forth. In the [HI] (and Hansen) data there are four variables, giving rise to four possible places where data averaging may have occurred to produce false data. A computer function was written see Appendix 1 which took each record with extra digits for height and compared values of the four variables to averages of all other unique pairs of records (of which there are 59(58)/2 = 1711).
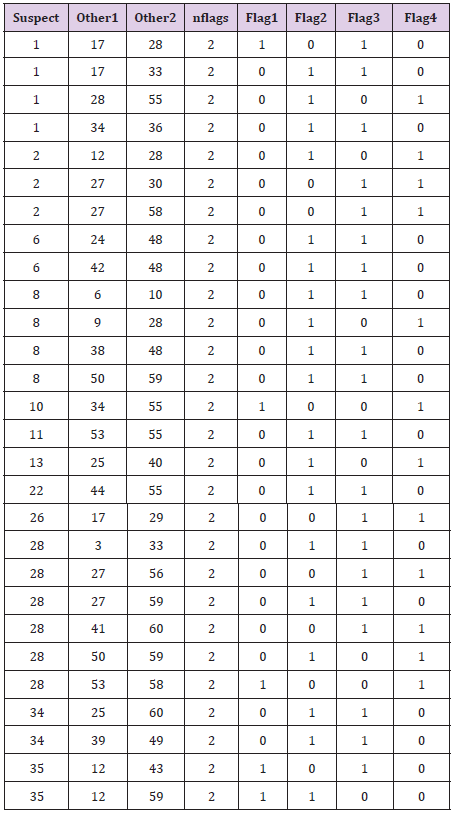
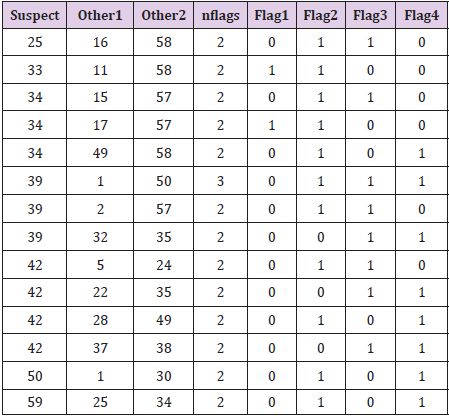
Each instance in which any of the variables in the “suspect” record with extra digits was found to correspond to the average of two other records was saved. Of the 18 suspect records in the [HI] data, pairs of other subjects were found such that the average of exactly one variable in those records matched the value in the suspect record in 17 cases. For 12 of the suspect records pairs of other subjects could be found that, when averaged, produced the values in the suspect record for exactly 2 variables. But for none of the suspect records was it possible to locate a pair of other subjects that when averaged produced 3 or all 4 of the variables in the suspect record. The results for suspect records having at least two variables equal to the average of other records are presented in Table 7. In this table, the column labeled “suspect” gives the subject number from the original data corresponding to a data record having extra digits for height. The columns labeled “other 1” and “other 2” give subject numbers from two other records that were found to average to the suspect record value for two or more of the variables. The column labeled “nflags” gives the number of variables (out of the 4 possible but at least 2) for which the two other records produced averages equal to what was reported for the suspect record, and the columns labeled “flag1” through “flag4” give the specific variables for which averages matched the value of the suspect record (flag1=height, flag2=weight0, flag3=weight1 and flag4=weight2).There are several aspects of the results in Table 7 that are of interest.
a) Note first that there are quite a few of the records with extra digits for height (12 out of 18 to be exact) that have at least two variables equal to the averages of two other records in the data set.
b) Curiously, many of the suspect records in Table 7 contain variables that have values equal to the average of more than one pair of other records (e.g., suspect record 1, 2, 6, 8).
c) The number of suspect records that have values equal to averages of other records seems more prevalent for weight variables than for the variable of height.
d) There are no suspect records that are are the same in total (i.e., for all four variables) to averages of other records. In fact, there does not appear to be a simple pattern for which variables are averages of other records. For example, subject numbers 17 and 28 as well as subject numbers 17 and 33 average to the value of weight1 for subject number 1. Subject numbers 17 and 28 also average to the height value for subject 1, but subject numbers 17 and 33 do not, while subject numbers 17 and 33 average to the value of weight0 for subject 1 but subject numbers 17 and 28 do not.
Overall, the results of Table 7 indicate that, if the suspect records with extra digits for height in the [HI] data were constructed using a process of averaging other data records, this was done according to some complex system that is difficult to uncover. For example, subject 1 had matches (i.e., flags) that involved subject numbers 17, 28, 33, 55, 34 and 36. The record for subject 1 was not a match for the average of any 3 of these other records (of which there are 20), any 4 of these records (of which there are 15), any 5 of these records (of which there are 6) or all 6 of the records. The number of instances in which some variables in the records for which height contained extra digits turn out to be equal to averages of other records is, however, curious. To examine whether or not the phenomena of Table 7 should be considered “out of the ordinary”, I compared the results given in that table with data generated randomly from a coherent probabilistic structure. To accomplish this, 60 records were simulated from a four-dimensional multivariate normal distribution with means, variances, and covariances equal to the realized values from the [HI] data set. This data set, then, was simulated to match the marginal and joint data structures of the [HI] data set, but to be a case in which other aspects of the data followed a typical probabilistic structure difficult for humans to duplicate if asked to purposely falsify data (this entire simulated data set is contained) in Appendix 2.
The four variables in the simulated data will be called height, weight0, weight1 and weight2, in analogy with the actual problem. Each simulated record was then rounded to the nearest whole number. Following the frequencies of Table 6, 18 values for the variable height were randomly selected to have an extra digit added to their values; to 5 records the value of 0.25 was added, to 9 records the value of 0.50 was added, and to 4 records the value of 0.75 was added. In addition, 11 records were randomly selected to have a value of 0.50 added to weight0, another 9 records randomly selected to have a value of 0.50 added to weight1, and 3 records were randomly selected to have a value of 0.50 added to weight2. Running these simulated data through the same computer function used to produce Table 7 from the [HI] data gave the results presented in Table 8.
Although there is a minor difference between the values of Table 8 and those from the [HI] data of Table 7 (i.e., 7 of the 18 “suspect” records in the simulated data matched averages of other records in 2 or more variables, while 12 of 18 did for the [HI] data) the patterns are remarkably similar. In fact, the second, third, and fourth characteristics of the data in Table 7 listed previously, which may have seemed suspicious, were reproduced nearly identically in the simulated data results of Table 8. Neither Table 7 nor Table 8 report the number of “suspicious” records matching averages in only 1 of the four variables. A table of frequencies for the number of suspicious records (out of 18 for both the [HI] and simulated data) that had 1, 2, 3, or 4 of the variables height, weight0, weight1, and weight2 matching averages of pairs of other data records is presented in Table 9. An ordinary Chi-squared test of differences for these frequencies is not appropriate here as the entries in Table 9 are not independent (i.e., a given suspicious data record could have matches with multiple pairs of other records, some pairs matching 1 of the variables and other pairs matching 2 of the four variables). In addition, only one simulated data set is presented, and other simulated data sets would vary from this one to some degree.
Table 8: Data records in a simulated data set with heights recorded with extra digits for which variablm were found to equal averages from two other records.
Table 9: Frequency of matches for “suspicious” data records with averages of other pairs of records for the [HI], Hansen, and simulated data sets.
The point of Table 9, however, is that it does not appear that the [HI] data are at all unusual compared to what might result from a completely random probabilistic mechanism with the same marginal and joint data characteristics. The only conclusion that seems plausible is that the patterns exhibited in the [HI] data and reported in Table 7 are entirely in concert with what might occur from a completely probabilistic structure matched to the marginal and joint structures of those data. It may also be of interest to examine the purportedly falsified Hansen data in the same manner as presented in Table 7 for the [HI] data and Table 8 for the simulated data. In these data, 7 records for “height” contain an extra digit of 0.50. Of these 7 records all 7 matched averages of other pairs of data records for 1 of the four variables, and 4 matched averages for 2 of the four variables, as indicated in the final row of Table 9. Thus, the Hansen data seem to follow the same pattern exhibited by both the [HI] and simulated data. It is not clear what exactly should be made of this, other than that the Hansen data appear to have much the same behavior as the [HI] data with regard to averaging, and both have behavior similar to randomly simulated data as well.
Distributions of Digits
There exist demonstrated distributions for the frequencies with which different digits (0 through 9) appear in data from various sources. None of these is applicable to the current situation, and this subsection is included to indicate why this is so. There is a result known as Benford’s law that indicates the relative frequencies of leading digits in data should follow an approximate logarithmic distribution e.g., Buyse et al. [1], Hill 2008. This approximation often applies to financial data and other data consisting of an aggregation of various sources but does not typically apply to scientific data from a single data source (e.g., Hill 2008). In fact, a proof that Benford’s law corresponds to a coherent probabilistic structure made use of random digits selected from random distributions Hill [5], a context that does not apply to most scientific investigations. The emphasis put on Benford’s law by, for example, Buyse et al. [1] seems misplaced, except perhaps in the examination of financial records for medical facilities.
The other use of distributions of digits in data to detect anomalies rest on the assumption that recorded data values may contain meaningful and nonmeaningful digits. The leading (first) digits of data values are often meaningful in indicating the magnitude of responses. The trailing (last) digit or digits are often nonmeaningful in this regard. For example, in a weight difference of 190.3 and 185.6 pounds, the first three digits of 190 and 185 are more meaningful than are the trailing decimal digits of 3 and 6. It is often assumed then that the meaningless digits should follow a uniform distribution on the discrete integer values from 0 to 9. Because the human mind appears to be a poor random number generator, fabricated data may often show a distribution of meaningless digits substantially different from a uniform distribution e.g., Walter et al. [3]. But, as pointed out by O’Kelly [6], data with non-meaningful trailing digits are relatively unusual in most clinical trials, and that is the case here except for perhaps the data records with extra recorded digits, which have already been examined in the previous subsection.
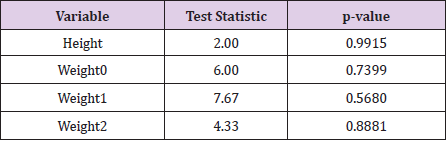
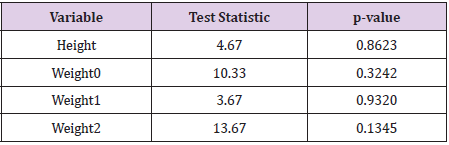
Nevertheless, in order to demonstrate what an examination of trailing digits would suggest about the three data sets currently under investigation (the [HI] data, the Hansen data, and the simulated data) I wrote a computer function to give the frequency of final digits (as whole numbers – data records containing extra digits first had those digits removed) for each of the variables of height, weight0, weight1, and weight2, and to test the resultant empirical distributions against a theoretical uniform distribution. The results for the [HI] data are presented in Tables 10 & 11. Under an assumption that the relative frequencies of final digits (0 through 9) should follow a uniform distribution, the expected frequency for each digit is, with 60 observations 60/10 = 6.0. Standard Chi-squared tests of goodness of fit for such a uniform distribution to the values in Table 10 yields the results of Table 11. Clearly, none of the variables contain distributions of final digits coming even close to having evidence of departure from a uniform distribution. Repeating this exercise with the data simulated from a multivariate normal distribution yields the observed frequencies of Table 12 and the associated test statistics and p−values of Table 13. These simulated data, as they should, also offer no evidence of a departure from a uniform distribution of final digits for any of the four variables.
Table 11: Test statistics and associated p-values for testing that the frequencies of final digits in the [HI] data differ from a uniform distribution.
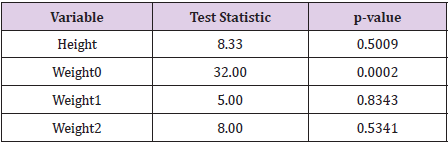
Finally, conducting the procedure once again for the Hansen data produces the observed frequencies of Table 14 and the associated test statistics and p−values of Table 15. In this case, it would appear that the final digits of 0 and 5 appear with sufficiently greater frequency than expected (in combination – neither frequency would be sufficient by itself) than other digits to result in evidence that for the variable of weight0 that final digits differ substantially from what would be expected under a uniform distribution. Whether this is, or is not, truly meaningful could be a matter of debate. No such evidence is present for the other three variables of height, weight1 or weight2. While this is certainly a curious feature of the Hansen data, I would be reluctant to attach too much meaning to this result if I had not been informed that the Hansen data were fabricated. This one lone test statistic, in the face of internal consistency as demonstrated in Section 3 and consistency with the averaging property of Section 4, would seem scant evidence on which to base a declaration of falsification. While certainly curious as compared to the results for the [HI] and simulated data sets, it seems one would need to be “reaching for straws” to conclude that this offers real evidence that the Hansen data have been falsified. The upshot of this subsection is that, in the first place, the examination of any of the data sets ([HI], Hansen, or simulated) for assumed distributions of digit values in either leading or trailing places could prove problematic on theoretical grounds. There is no solid reason to assume that any of these data sets (aside from the simulated data) should exhibit any particular distribution of digits in any order, other perhaps than that weights should not have leading digits less than 1 for overweight individuals (i.e., less than 100 pounds) and would be unlikely to have leading digits greater than 3, even for a sample of offensive linemen from the national football league. That the trailing digits of the Hansen data set appear to have some departure from a hypothesized uniform distribution for the variable weigth0 certainly is of interest, but also is certainly not definitive in offering evidence of falsification.
Table 13: Test statistics and associated p-values for testing that the frequencies of final digits in the simulated data differ from a uniform distribution.
Table 15: Test statistics and associated p-values for testing that the frequencies of final digits in the simulated data differ from a uniform distribution.
Could the [HI] Data Be Simulated?
The agreement of the [HI] data with values simulated from a multivariate normal distribution in terms of the averaging phenomena discussed in section 4.1, and the distribution of trailing digits in Section 4.2, raises the question of whether the data could have been produced wholesale (i.e., in entirety) from the use of a random number generator. The most likely candidate for such simulation would be a multivariate normal distribution with marginal and joint characteristics equal to the means, variances, and covariances reported for the [HI] data and described in Section 3 of this report. Given a moderate amount of statistical sophistication, anyone could produce such a data set. That this is unlikely to be the case in the current situation is evidenced by the failure of marginal distributions of weight0, weight1, and weight2 to follow univariate normal distributions. A known property of multivariate normal distributions is that the marginal distributions corresponding to individual variables are univariate normal in form.
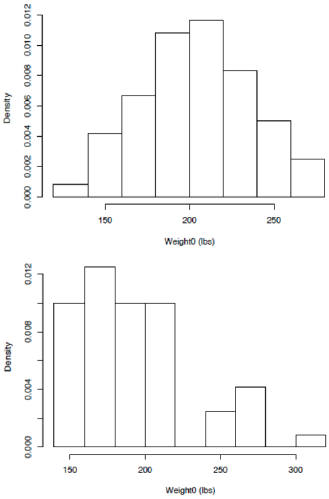
Figure 4 presents histograms of the marginal distributions of weight0 for the simulated data set in the upper panel and the [HI] data set in the lower panel. The simulated data (upper panel) exhibit a distribution consistent with a normal theoretical distribution, which they should. The [HI] data (lower panel) exhibit a distinct skew right distribution, consistent with the observation of the scatterplots of weight versus height in Figure 2 (see Section 3 of this report). Is it possible to simulate data that have the characteristics of the [HI] data set? The answer is yes, it is possible, but doing so would require the ability to preserve means, variances, and correlations as described in Section 3 of this report, preserve the averaging property described in Section 4 of this report, and produce the difference in marginal distribution of weights at time 0 given in Figure 4. There exist ways to achieve all of this, but they require a relatively high level of statistical knowledge, including the time and ability to write computer functions for tasks that are not readily available in pre-packaged routines.
Figure 4: Histograms of weight at time 0 for the simulated data set (upper panel) and the [HI] data set (lower panel).
Influence on Results
Falsification of data often has the objective of producing certain results in a data analysis. Quantification of the influence of each observation on the resultant analysis can then sometimes highlight one or a group of observations that played a large role in determining the outcome and conclusions of a study. While not in any manner evidence of falsified values by themselves, the occurrence of high influences can suggest cases worthy of additional examination. In the report on results of the [HI] study provided to me, the analysis consisted of two paired t-tests, one conducted on the difference in weight0 and weight1 values and the other conducted on the differences in weight1 and weight2 values. To examine the influence of recorded data values on these tests I simply deleted observations one at a time from the data, recomputed the test statistic without that value, and took the difference (absolute value) of that deleted-case statistic with the test statistic computed using the entire data set. This value then provides an indication of the influence of individual observations on the test conducted with the entire set of values. A summary of the influence values produced using the [HI], Hansen, and simulated data for the comparison of weight0 and weight1 values is presented in Table 16, and the same is reported for the comparison of weight1 and weight2 values in Table 17. The most notable feature of both Tables 16 & 17 is the extreme distance between the third quartile (or 75%−tile, denoted Q3) of influence values and the maximum influence value for the [HI] data in both Tables 16 & 17, and the Hansen data, at least in Table 16. Stem and leaf plots demonstrate that this is due to only one extreme value that is hugely separated from the remainder of the data. For example, the influence values for the [HI] data of Table 16 have the following stem-and-leaf plot: The decimal point is at the (Figure 5).
The data record that corresponds to the single observation with influence value 2.8 (which is just over 9 times larger than the next larges value) corresponds to subject 52 having height= 66, weight0= 186, weight1= 189 and weight2= 192. This subject gained weight between each weighing. The result is that, while highly influential relative to any of the other data records, the results for this subject decreased the size of the test statistic and hence the significance of the overall findings of the study. If this record was falsified the only reasonable objective would have been to purposely introduce one outlier into the data to make it look more “real”, not to produce a desired result in the analysis of the study. This same observation is also the one extreme influence value for the [HI] data from Table 17.
Curiously, the Hansen data also contain exactly one such record, for what would be subject 45 in those data, with values height= 72, weight0= 275, weight1= 277 and weight2= 279. I surmise at this point that the Hansen data were not fabricated from scratch but, rather, took the [HI] data as a template to which various modifications were made in a haphazard but more-or-less “symmetric” manner. This would explain the close correspondence between marginal and joint data distributions for the [HI] and Hansen data and the reason the Hansen data appear internally consistent (see Section 3). If those modifications were made haphazardly (i.e., by simply switching records and writing down different trailing digits in a seemingly haphazard manner) then this would also explain the trailing digit preference for weight0 seen in the Hansen data although, again, I hesitate to make too much of this occurrence.
Conclusions from the Drs. K and C Statistical Analysis
As stated in the opening paragraph of this report, a statistical examination of data cannot definitively prove or disprove the falsification of data records. The analysis conducted in this report, however, does allow the following conclusions to be comfortably reached.
a) If the [HI] data were falsified it would appear that they were fabricated in a nearly wholesale fashion, that is, more-orless in total. These data are internally consistent, consistent with the behavior of values simulated from a theoretical probability distribution, and there is only one data record with undue influence on the results of the study (and this influence was in the “wrong” direction).
b) Because of the properties listed in conclusion 1 and, in particular, the averaging behavior described in Section 4 that the [HI] data shared with simulated data, the most likely mechanism for fabrication in this study must be considered simulation from some theoretical probability model.
c) Because of the multivariate nature of the four recorded data values for each subject, maintaining internal consistency would require, or at least strongly suggest, that a multivariate probability distribution would need to have been employed to simulate data values. The candidate most readily available to non-statisticians (and even to statisticians without extensive experience in the construction of multivariate distributions from other probability structures) is the multivariate normal distribution.
d) The marginal moments (means, variances) and joint moments (covariance or correlation) of the [HI] data could easily be maintained through simulation from a multivariate normal distribution. However, the skew shape of marginal weight distributions e.g., Figure 4 could not.
e) Combining items 1 through 4 immediately above suggests that, if the [HI] data were fabricated, the procedure used to arrive at the reported values was necessarily complex, requiring considerable statistical expertise and time to conduct. If it were supposed that the most likely motivation for data fabrication in this situation was to save time and effort relative to actually performing the observational process, this would seem at odds with what would have been needed for fabrication of the data.
f) Finally, the Hansen data represent an interesting construction if they were produced from scratch, but much less so if they were produced through modification of the [HI] data. If they were produced from scratch, they achieved remarkable success in preserving marginal and joint data structure and relative evenness in influence (either through chance or design). If they were produced through modification of the [HI] they simply borrowed these properties from values that already possessed them. My suspicion is that these values were obtained by either modifying the [HI] data or, at the very least, using those data as a template for construction. The one property expected of actual data that could not be entirely maintained in the Hansen data was a uniform distribution of trailing digits in recorded values, although whether this is a valid criterion for the current situation is not entirely clear, as explained in the section on Distributions of Digits.
Overall, there is simply no data-driven evidence that the [HI] data set is other than would be expected under a legitimate study. While there are several aspects of the Hansen data set that might cause concern, there is no definitive indication that these data were fabricated either, absent the knowledge that this was the case. This would not be unexpected if the Hansen data were patterned after the [HI] data, but if the Hansen data were fabricated from scratch they should be preserved as a case study against which to test statistical methods of unusual patterns in falsified data. If the Hansen data isn’t fabricated, could it represent plagiarism of the HI data?
Given the statistical analysis by Drs. K and C, the [HI] data showed no evidence of being anything other than genuine data from an authentic study; free of data fabrication. While Drs. K and C expressed concern multiple times in their report, that the Hansen data appeared to be falsified or patterned after (template) the [HI] data, they did not analyze the Hansen data for actual falsification or plagiarism as they were instructed to look only for data fabrication. Hansen himself had stipulated to Drs. K and C that the Hansen data was “entirely fabricated.” Drs. K and C consequently developed multiple statistical programs, using one of the top statistical laboratories in the world to do so, to determine if either the [HI] or Hansen date had in fact been fabricated.
Absent the ability to find data fabrication in the Hansen data, Drs. K and C were left with one of two possibilities. First, their statistical methods, which appeared to work on the HI data and clearly worked on the “simulated” data, did not detect data fabrication in the Hansen data. Under this premise, Drs. K and C concluded that the Hansen data “should be preserved as a case study against which to test statistical methods of unusual patterns in falsified data.” The second possibility, given their statistical analysis was that the Hansen data had somehow been plagiarized from the [HI] data itself. This seemed the most likely answer and although Hansen chose to stop the statistical analysis of his data set by Drs. K and C, we asked for others to investigate the possibility that the Hansen data, as suggested by the statistical analysis of Drs. K and C, might actually be data plagiarism, explaining why analysis focusing on fabrication would have been unable to fully uncover the Hansen fraud.
Here the analysis of the Hansen data by Drs. K and C ended and a shift in the statistical investigation of the data looking for data plagiarism by Hansen from the [HI] data to produce the Hansen data. To statistically analyze the Hansen data for plagiarism, Dr. H further analyzed the data sets utilizing statistical methods well known to him as discussed below. The Dr. H. Report was submitted directly to Hansen. After a failure of Hansen to respond, Dr. H’s letter was later sent to the primary author. As noted in the report, Dr. H. tested for data fabrication, falsification and eventually data plagiarism.
In keeping with the method used here, we will let Dr. H’s letter to the primary author explain his analysis in his own words through the correspondence associated with his investigation of the Hansen data.
Part II: The Dr. H. Report – as Written by Dr. H.
Dear []:
You inquire about my analysis of [the HI] data and of the Hansen data. Neither was ever provided to you. Using well-established methods, I made multiple fabrication tests of [the HI] data. There was no evidence of fabrication. Drs. C and K used complex methods for detecting fabrication recommended by the Government agency responsible for developing such methods and for overseeing their use in PHS agencies. They found no evidence of [HI data] fabrication. I found the Hansen data were plagiarized, as later confirmed []. I found the Hansen data to be falsified, as later confirmed []. The law establishes three forms of data fraud: fabrication, falsification, and plagiarism. [It was suggested that HI had fabricated data] and all the tests show there was no [HI data] fabrication.
It may be best to provide some commentary on my statistical background. My prewar experience had been high school dropout to take a manufacturing production line job. It was the depths of the Depression. We were on welfare. Night school (Electrical Engineering, Georgia Tech) led to employment in the Electrical Engineering departments of a power company and then a telephone company. My professional involvement with statistics began with my first job upon returning from three years WWII Naval service. It was at Georgia Tech doing statistical analyses for corporate studies in industrial psychology in the Psychology Department, the beginnings of my involvement in psychology. The following year brought an appointment to the Mathematics faculty. In 1949-50 I became a student in a one-time applied statistics program at Yale, taught by the world’s top statisticians as visiting professors. It was my good fortune to be assigned as a graduate assistant to Sir Ronald Fisher, universally regarded as the greatest statistician of all time. Not only was Fisher the Father of modern statistics, he was also the Father of modern population (quantitative) genetics which is how I got into neuro-behavioral genetics.
Also on the visiting faculty were Frederick Mosteller and Philip Rulon of Harvard. Many regard Mosteller as the greatest statistician of the second half of the 20th century. Rulon held the Measurement chair at Harvard. In 1951 I went to Harvard as a post-doc with Mosteller and also worked in a Harvard affiliated research institute led by Rulon and American Association for the Advancement of Science President Kirtley Mather. There I was Project Director on two contracts, one in air traffic control for the Air Force, the other for simulator combat training for flag rank Naval officers. Next was a research consulting slot with the State of Connecticut for educational and labor market studies. I held various professional offices, most interesting being the Presidency of the Connecticut Chapter of the American Statistical Association. Connecticut had a high population of insurance statisticians (actuaries) as the Insurance State, of industrial statisticians (quality control engineers) as the high tech manufacturing center where mass production originated (clocks and arms), and of financial statisticians (accountants) as the leading commuter residential State for the New York banking industry.
Two of my Executive Committee went on to Nobel Laureates in Economics (Tobin and Koopmans). I also served on an Institute of Mathematical Statistics Committee on Standards for Training of Statisticians. My career moved to academe in 1957 where I formally retired in 1986. I was named Distinguished Scholar at the University of Northern Iowa. I have been a regular reviewer for a number of scientific journals here and in Europe and for the National Institutes of Health and the National Science Foundation. After over two decades of retirement I have been accepting review requests less frequently. You contacted me for [statistical analysis regarding a study involving HI where] “some of the data were fabricated” in a [snack food] study of 60 research participants. More specifically you indicated it was known that some of the data were genuine but alleged later data were fabricated. I replied fabrication of data is a matter of great current interest in the financial community, the intelligence community, and the health research community. My advice was that you should contact the Office of Research Integrity to ascertain what, if any, assistance you could obtain from them.
They were established as the Federal Agency responsible for developing methods for detecting lack of integrity in research data and were touted in the statistical world for their contributions. They inherited some of the FBI experts in data fraud but early reports on formation of the ORI were not clear on the scope of their mission which was asserted to be Government wide on data fraud research and education but limited to PHS activities in investigatory authority. [My] suggestion was [for you to contact] Dr C who has a high reputation and who teaches forensic statistics at [] has long been regarded as one of the top half dozen statistical institutes in the world.
You told me [Hansen] regarded statistics as worthless [and] any good lawyer could destroy statistical evidence. I commented my accountant brother who is operating vice-president of a financial house and on multiple boards of directors would be horrified to learn that any good lawyer could destroy the results of any audit. You indicated [Hansen and his associates] held similar negative views of statistics. I am skeptical. My experience has been of lawyers trying to make statistics sound worthless only to have the judge chastise them with a lecture on statistics. My experience is not extensive, but I have testified a few times. According to the [] many years ago I was the witness who brought regression analysis into the judicial system as a standard method for assessing race and sex discrimination in wages and salaries. Some of the lawyers betrayed little competency in statistics. The judges I have encountered were more knowledgeable. When I expressed surprise once after trial at how much the judge knew he commented it was the job of judges to learn what they needed to know and he had obtained a crash education in statistics because he was the judge who heard the great redistricting case [7,8].
The difficulty with statistics is that a type of reasoning is required to which people are not accustomed. The fundamental basis of statistics is that the universe is governed by the laws of chance. The less scientifically educated can be misled, as [Hansen] suggests, by the fact the statistician will not say with certainty that something is or is not so. The statistician’s work is based on the fact there is no certainty. [] There are studies on the levels of chance people ascribe to these terms. I have seen appeals court decisions remanding for failure to include the quantitative levels of probability in the court record. In the abstract we may identify a connection and prove if A then B but in the real world the exact proof is that if A then B plus or minus e. In popular parlance there is a margin of error. Statisticians are by the nature of their profession aware of error where most people are not. For example, people tend to think of computers as giving unquestionable calculations. However, A times B equals C is actually A times B equals C plus or minus e. The margin of error is small but real. Forty years ago, the National Bureau of Standards developed very complex algorithms for very simple arithmetic operations such as multiplication for the purpose of reducing that margin of error (NBS Special Publication 339, 1970). Other algorithms verified error levels in very complex calculations. I still use them occasionally and decry their absence from contemporary software packages.
The detection of research fraud rests on three basic scientific realities. The universe is governed by the laws of chance; hence we can test whether data follow the laws of chance or are fabricated. The phenomena of the real-world result from many factors interacting with each other. The National Transportation Safety Board needs months to run down the specific factor or factors leading to a crash. The Mayo Clinic may run a hundred tests to discover why a body is not functioning properly and additionally consider their relationships to each other. Physiology and behavior vary statistically with differing genes and environment. To avoid detection the fraud perpetrator must be able to anticipate which tests and which interrelationships will be tested and design data which will pass those tests. [Clearly this was not possible given the development of Drs. K and C statistical programs more than 5-years after the snack food study was completed.] The third and never mentioned fact is that Pavlovian conditioning and operant conditioning were displaced by the discovery about half a century past that the human nervous system cannot manage ten concurrent concepts. Our air safety research revealed that airplane accidents stemmed from too much information—one can tell time more readily with a four number otherwise blank dial than with a face showing 60 tick marks. Weather maps went from detailed measures and locations to five or at most six-color displays. The keep-it-simple principle was born.
You sent me [the HI] data as being effects of a [snack food study] in a sample representative of U.S. adult males and females selected for obesity. It was alleged earlier participants were real but later ones were fabricated. This fitted the paradigm of standard industrial quality control. Quality control engineers test and statistically track products monitoring whether products show trends away from statistical expectations and specifications. Trends or deviations signal underlying production factors have changed leading the engineers to investigate to determine what changed and to correct the problem. The allegation that the underlying factors changed from dieter response to fabrication seemed a perfect fit. For three quarters of a century it has been conventional to display the statistics in the form of charts showing the sequential measurements and boundaries of expected margins of error. The methods originated with W. Edwards Deming (one of the Fathers of survey and census methods and the progenitor of Japanese manufacturing production and quality control methods) and with Walter Shewhart for whom the charting method is named. I tested [the HI] data and found no evidence of changes in the data, hence, no evidence of fabrication. For reasons cited above that fabrication is very difficult and because Shewhart charting has long been well established and successful as the basis for quality control I concluded there was no evidence of fabricated data. You forwarded my assessment to [] Hansen.
[] Hansen wrote me it is impossible to tell whether data are fabricated on the basis of examining the data. (I was tempted to point out the recent major fraud cases in which the primary evidence was the CPA audits.) He indicated he could easily fabricate data so that it could not be detected. He indicated he would do so and send me a data set comparable to [the HI data] and challenged me to use my Shewhart methods to show his data were fabricated. He particularly emphasized that he had written an undergraduate thesis on Deming and fully understood the concept. As I recall there was an e-mail explicitly stating the issue was that earlier [HI] data were valid, and the balance of the data were not.
I tested the Hansen data set as I would as a journal reviewer. I reported that the first three tests each showed [Hansen] data were falsified or, more precisely as a journal reviewer, they were not what they were represented to be. Specifically, the results showed the [Hansen] data were not representative of the population to which inferences were to be made. For journal reviewing I would have stopped at that point, rejecting the manuscript and leaving it to the Editor to decide whether to investigate it as falsification or conclude the sampling procedures were defective.
As requested, I did apply the Shewhart methods and reported to [] Hansen they showed no fabrication. Since he had clearly stated he understood the method would test whether some of the data were genuine and the balance fabricated, since he had prepared the data, and since the data tested as not being fabricated, it was evident he knew the data were not fabricated. It seemed impossible [] Hansen could have obtained such data elsewhere so the data must be falsified [HI] data. A plagiarism test was statistically significant in the range of seven orders of magnitude. In layman’s terms the chances the Hansen data were not plagiarized from the [HI] data are less than one in ten million []. I saw no need for further plagiarism tests. At the time I concluded Mr. Hansen’s intent was to test my analysis of the [HI] data to see if I arrived at a different conclusion when I was led to believe the data were fabricated. We communicated no further.
In all I made nine fabrication tests on the [HI] data and nine on the plagiarized Hansen data. None of these 18 tests showed any evidence of fabrication. All three falsification tests showed the Hansen data had been falsified. The plagiarism test speaks for itself. Fabrication, falsification, and plagiarism are the three forms of health data fraud defined by statute.The report [by Drs. K and C] represents a totally different approach than mine. It follows along the lines suggested by the Office of Research Integrity. The ORI is the Governments agency for developing best methods for detecting research misconduct which would seem to establish its methods as a Government established standard.
I note, inter alia, that the report [by Drs. K and C] speaks of difficulties with the Hansen report []. My reading of the report is that [Drs. K and C] were puzzled by the Hansen report because they could find no evidence of fabrication when they were told [by Hansen that] the data were [entirely] fabricated. They explicitly excluded falsification tests, justified by that information [they were provided] but which I regarded as something of a deficiency. []
In summary I audited the [HI] data using a number of standard industrial quality control tests to determine whether some of the data were genuine and some fabricated. There was no evidence of [HI data] fabrication. I similarly audited the Hansen data finding no evidence of fabrication. I applied several tests to see if the data were representative of the defined population group. The [HI] data were. The Hansen data were not, suggesting falsification. A comparison test showed the Hansen data were plagiarized from the [HI] data. Falsification tests rest on the effects of a large number of underlying factors. Falsifying the numbers for a few of those factors alters little of the underlying factor effects. The assessment of no evidence for fabrication of research participants in the Hansen data simply provides a confirmation of lack of evidence of fabrication of research participants. The [Drs. K and C] report [] represent an entirely different and more complex set of tests for fabrication following the recommendations for testing for fabrication of the Federal agency charged with developing and promulgating such testing methods. With their entirely different approach from mine they also found no evidence of fabrication of the [HI] data and confirmed that result with the Hansen data. For report [] they were asked to respond only to the charge of fabrication. They were not asked to [address] either falsification or plagiarism and did not do so.
As I said at the beginning: Using well established methods I made multiple fabrication tests of [the HI] data. There was no evidence of fabrication. [Drs. C and K] used complex methods for detecting fabrication recommended by the Government agency responsible for developing such methods and for overseeing their use in PHS agencies. They found no evidence of fabrication. I found the Hansen data were plagiarized []. I found the Hansen data to be falsified []. The law establishes three forms of data fraud: fabrication, falsification, and plagiarism. [All] the tests show there was no fabrication [of the HI data] with plagiarism and falsification of the Hansen data.
Part III: The Actual HI and Hansen Data Side by Side
One has to wonder the motives behind Hansen and his data. Was it criminal, arrogant or was there some other motive? According to Hansen, he originally submitted his plagiarized data set to Drs. K and C to prove that statisticians could not prove data fraud. Consequently, Hansen misrepresented the facts to Drs. K and C, telling them his data – the Hansen data - was completely fabricated. As a result, Drs. K and C only developed statistical tests for fabrication. One then has to wonder, why when the data was under investigation, Hansen then proceeded to instruct Dr. C to remove the Hansen data from the final report, so his name and plagiarism of data would not be discovered. One then also has to wonder why the final arbitrator participated in the cover up, preventing the Hansen data from being brought forward and being exposed – thereby proving the tests developed and carried out by Drs. K and C validated the HI data as valid.
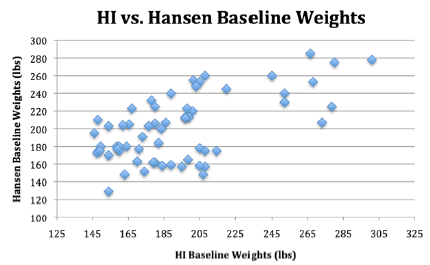
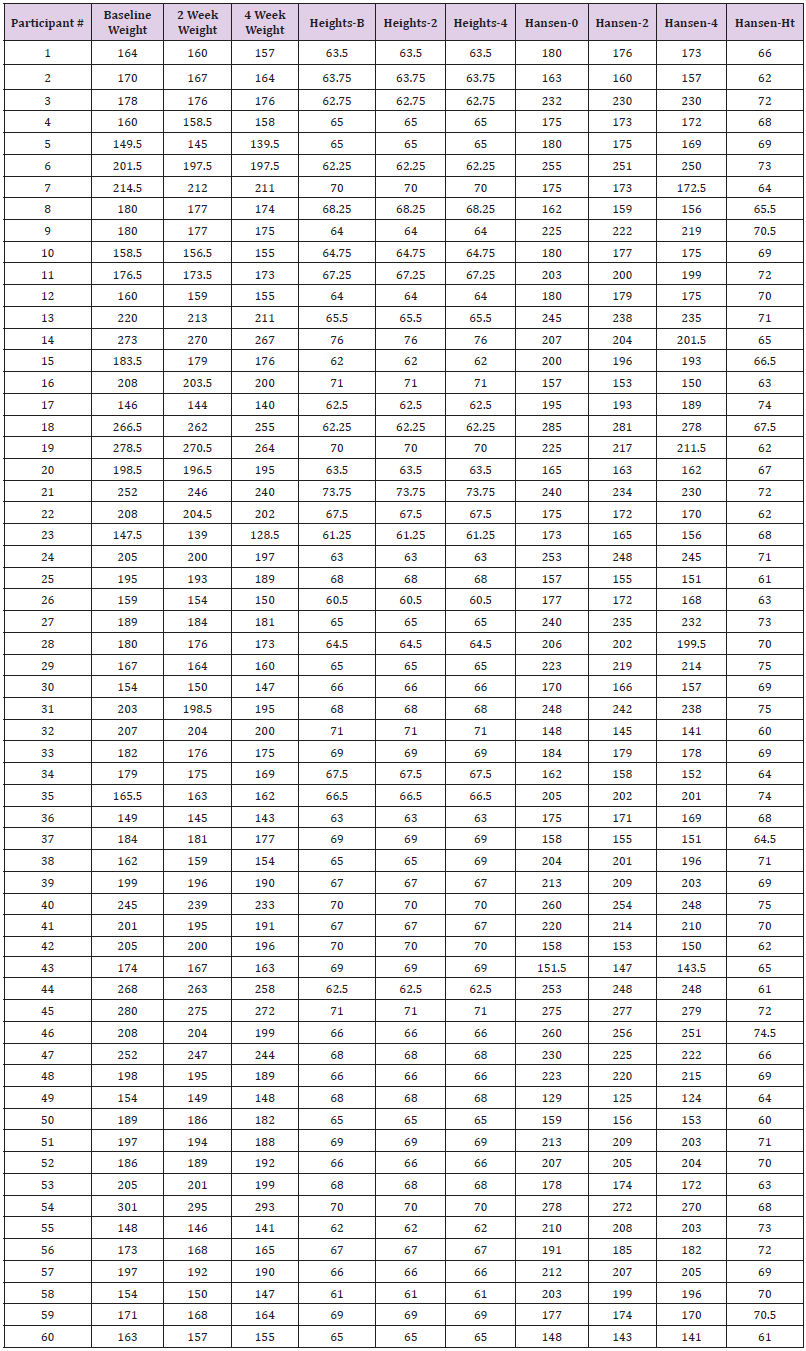
Table 18 shows the side-by-side comparisons of the HI and Hansen data. Hansen reported that he merely took the HI data and used it (plagiarized) by adjusting the heights for his data and then calculating the weights according to BMIs. He then rearranged the data in his report, so the patient numbers no longer matched. It would be very interesting, for those with more statistical expertise than the authors, to specifically show and report on how Hansen plagiarized the HI data. It is clear that Hansen is not inclined to publically admit what he has done, and Dr. C has now expressed fear of coming forward to address this herself. Finally, the changes in HI weights graphed out at baseline, 2-weeks and 4-weeks are mirrored by the Hansen changes in weight. This almost identical pattern of change for Hansen data matching the HI data provides more empiric evidence of plagiarism by Hansen (Figures 6-8).
Table 18: The original HI data represented as Baseline Weight, 2 Week Weight, 4 Week Weight and Heights-B, 2 and 4. The baseline Hansen data is noted as Hansen-0, with the 2 and 4-week weights in the next columns followed by the Hansen - Ht.
Overall Conclusions from The Three Sets of Statistical Analysis
Today it is recognized that there is an ever-growing problem with potential research fraud. While there are a number of individuals and groups who have expressed an interest in this topic, the primary motivation appears to be directed either at the retraction of papers, which tend to be associated with a disagreement between the position of the authors and the submitter of the complaint; a problem all too frequent and not deserving of a response other than the submission of a well-placed letter to the editor for publication in most cases; or the questioning of reproduction of figures in more than one paper.
Here people seem to be more concerned with whether an author has submitted a figure they have copyrighted in more than one paper; after all given copyright ownership of intellectual property under the U.S. Constitution, this is their intellectual property and as such they have the right to use it more than once. It is also much more important than a disagreement about what is and isn’t the absolute final truth in understanding a scientific question as this is the ever-present ongoing task behind scientific investigations. This is addressed through multiple publications over time in multiple journals and presentations at scientific conferences, best discussed in the light of day where legitimate scientific differences exist.
In this paper we are much more concerned with the intentional and knowing misrepresentation of data (Hansen data fraud) from which fraudulent conclusions are made. Here we are focusing our concern with revealing this data fraud through the use of scientifically established statistical analysis of data to expose fabrication, falsification and plagiarism of data and the efforts individuals will go to, to present their fraudulent data as something other than what it actually is. Here, through statistical analysis, the HI data was shown to be valid and the Hansen data was shown to be falsified and plagiarized from the HI data.
The process of addressing data fraud should begin with the submission of data prior to publication consideration and not post publication. Such acceptance of fraud should never be taken lightly. It is our scientific duty, both morally and ethically to determine what is and isn’t valid; what is and isn’t fraudulent. It is the obligation of each reviewer, editor, scientist and journal to prove data fraud through statistical analysis of the data, if there is a question of data validity and to provide that proof back to the authors, scientific community and the world. Acceptance of fraudulent data for publication is not a right and retraction once accepted without proof of data fraud is just a grievous an error as accepting a paper for publication without an analysis of the data in the first place.
The process of determining if something is fraudulent is clearly not always such an easy one as this paper has, we believe so clearly demonstrated. In this instance the original HI data, which opponents accused of being fabricated, turned out to be the real valid data and was vindicated through the use of statistical analysis. In contrast, despite efforts to the contrary, the Hansen data set was statistically shown to be falsified and plagiarized from the HI data.
Acknowledgment
The authors wish to thank the respective statisticians Drs. Mark S. Kaiser and Alicia L. Carriquiry of the Department of Statistics – Iowa State University, Dr. Gordon M. Harrington of the Department of Psychology -University of Northern Iowa and Dr. Ann A Hohmann ORI Scientist-Investigator. We appreciate Richard G. Kopf, Michael J. Hansen, Alan L. Everett, and Steven A. Russell for recording their sidebar agreement revealing their conspiracy to hide substantive exculpatory evidence from the Jury, Expert Witness and defendant, protecting the public defender, resulting in Ineffective Assistance of Counsel and Obstruction of Justice as evidenced in the sidebar recording (https://www.youtube.com/watch?v=Zu5YhxZO_WI&- feature=youtu.be). This paper is reprinted in part with permission of the primary author from the original material. The appendices are available upon request.
Conflict of Interest
No conflict of interest.
References
- Buyse M, George SL, Evans S, Geller NL, Ranstam J, et al. (1999) The role of biostatistics in the prevention, detection and treatment of fraud in clinical trials. Statistics in Medicine 18(24): 3435-3451.
- Al Marzouki S, Evans S, Marshall T, Roberts I (2005) British Medical Journal 331: 267-270.
- Walter CF, Richards III EP (2001) Using data digits to identify fabricated data. IEEE Engineering in Medicine and Biology 20: 96-100.
- Akhtar Danesh N, Dehghan Kooshkghazi M (2003) How does correlation structure differ between real and fabricated datasets? BioMed Central Medical Research Methodology 3: 18-26.
- Hill TP (1996) A statistical derivation of the significant-digit law. Statistics in Science 10: 354-363.
- Kelly M (2004) Using statistical techniques to detect fraud: a test case. Pharmaceutical Statistics 3: 237-246.
- Hill TP (1998) The first digit phenomenon. American Scientist 86: 358-363.
- Mosimann JE, Ratnaparkhi MV (1996) Uniform occurrence of digits for folded and mixture distributions on finite intervals. Communications in Statistics – Simulation and Computation 25: 481-506.

 Case Report
Case Report