Abstract
Molodtsov introduced a general mathematical theory, to addressing uncertain and undefined objects which is known as soft set theory. In this work, we study soft set with some definitions and operations, also discuss a soft set technique for order preference by similarity to ideal solution (TOPSIS) method and use this method for decision making.
Keywords: Soft Set; TOPSIS; Decision Matrix; Normalized Decision Matrix; Weighted Normalized Decision Matrix
Introduction
In recent time, classical methods are used to solve different problems which are faced in medical sciences, engineering, social sciences, etc. Many theories like fuzzy set theory, probability theory, rough set theory, etc. are used to solve these uncertainties, but these theories have their own problems which were attensioned by Zadeh. First of all, (Zadeh) in [1] initiated the concept of fuzzy sets by the extension of classical notion on sets. Nowadays fuzzy set theory is rapidly progressing, but cases, we face some limitations such as how to adjust the membership functions in this theory. Molodtsov proposed the concept of soft set to solve those problems which contain uncertainty in 1999 and defines a soft set as a parameterized family of subsets of universe set where each element is considered as a set of approximate elements of the soft set in the past few years of fundamentals of soft set theory studied by various researchers [2]. Various potential application in soft set in many areas like in smoothness of functions game theory operation research Riemann integration theory of measurement and so on are highlighted in Molodtsov.
In these days, mathematician plays a vital role in the soft set fuzzification. After the fuzzification of soft set, a new theory introduced which is known as a fuzzy soft set with different types and properties Maji et al. [3]. The soft set theory was reviewed [4] and used this theory for decision making, they also introduced different types of soft set with examples and defined some operations such as And-operation, Or-operation, union, intersection, complement, etc. on soft set [5]. In Chen et al. [6] redefine the idea of parameterization reduction in a soft set and compare it with a rough set, they also improve the applications of soft set by using a new definition in the decision-making problem. Some new notions on soft set Ali et al. [7] are introduced, such as restricted union, restricted intersection, restricted difference and extended intersection with examples and properties. Yeşim et al. used the fuzzy TOPSIS method [8] to select a supplier out of three suppliers in a company of garment operating in Turkey. Jahanshahloo et al. extended the approach of the TOPSIS method for decision making by the help of fuzzy data [9].
They also introduced a new concept of normalized fuzzy numbers with the help of α-cuts and applied this proposed concept on numerical problems. The Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) introduced in [10] to solve multi criteria decision making problems with different alternatives. In [11] Chen & Hwang extend the idea of the TOPSIS method and presented a new model for TOPSIS. He also used the newly proposed method for decision making to solve uncertain data in [12]. The authors used this method for the prediction of Diabetes patients in medical diagnosis. In [13-15], the authors presented the applications of fuzzy TOPSIS in different areas and used for decision making. Zulqarnain M and Saeed M [16] used the interval-valued fuzzy soft matrix in decision making. They also introduced a new decision-making method in [17,18] on interval-valued fuzzy soft matrix. In this paper, we discuss about soft set TOPSIS method and used this method for the selection of best candidates for bank jobs.
Preliminaries
Definition: 2.1 [2]
A pair (F, E) is called a soft set over a given universal set U, if and only if F is mapping of a set of parameters E, into the power set of U. i.e.
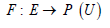
Clearly, an soft set over U is a parameterized family of subsets of a given universe U.
Also, for any p ϵ E, F (p) is considered the set of p –approximate element of the soft set (F, P)
Definition 2.2 [2]
Let (F, A) and (G, B) are two soft sets over the same universe U, then (F, A) is a soft subset of (G, B) if
A ⊆ B , and
For all t∈ A, F(t) and G(t) are an identical approximation
It is denoted by (F, A) ⊆ (G, B).
Definition 2.3 [5]
(F, A) and (G, B) are called equal soft sets if (F, A) ⊆ (G, B) and (G, A) ⊆ (F, B) . It can be written as
(F, A) = (G, B)
Definition 2.4 [19]
Let (F, A) and (G, B) are two soft sets over U, then their union is defined as
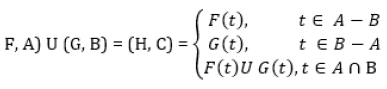
Definition 2.5 [19]
Let (F, A) and (G, B) are two soft sets over U, then their intersection is defined as
(F, A) ∩ (G, B) = (H, C)
H (t) = F (t)∩ G (t)for all t ∈ C, where C = A∩B .
Definition 2.6 [5]
Let (F, A) and (G, B) are two soft sets over the same universe U, then their restricted difference is defined as
(F, A) − R (G, B) = (H, C)
Where C = A∩B and for all t∈C , H (t) = F (t)∩ G (t)
Definition 2.7 [19,20]
A soft set (F, A) over a universe U is said to be a null soft set denoted by Φ if ∀e∈ A, F (e) = Φ.
Definition 2.8 [2]
A soft set (F, A) over a universe U is called absolute soft set denoted by (F, A) if ∀e∈E , F (e) = U .
Definition 2.9 [5]
If (𝐹, 𝐴) and (𝐺, 𝐵) are two soft sets then “(𝐹, 𝐴) 𝐴𝑁𝐷 (𝐺, 𝐵)” denoted by (𝐹, 𝐴) ∧ (𝐺, 𝐵) is defined by (F, A) ∧ (G, B) = (H, A× B) ,
Where H (α ,β ) = F (α )∩G(β ),∀(α ,β )∈ A× B.
Example
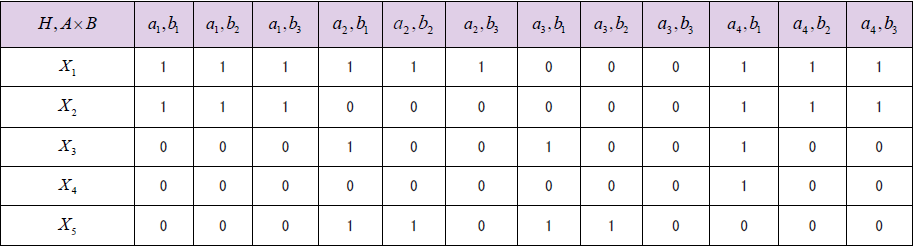
Let U = {x1, x2, x3, x4, x5} be a set of candidates in interview for job in the bank. Let A and B are two sets of parameters such that A= {a1, a2, a3, a4} where ai represents that the candidates are beautiful, tall, confident and brilliant respectively.
Let B = {b1, b2, b3} be a set that represents the qualification of candidates SSCE, BS, and MS respectively.
Then
(F,A)={f(a1)={x1,x2},f(a2)={x1,x2,x3},f(a3)={x3,x5 },f(a4)={x1,x2,x3,x4}}
And
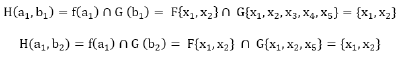
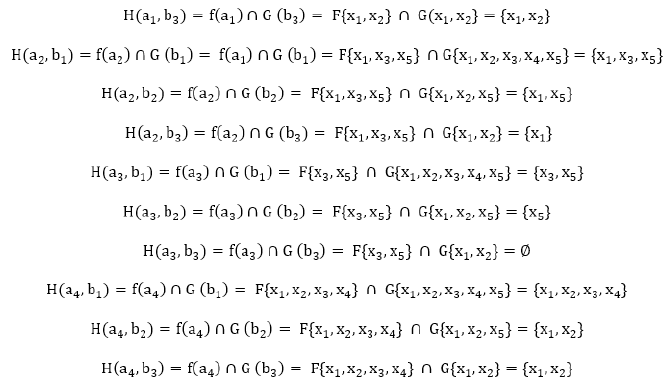
Now
a) Means beautiful applicant with SSCE are {x1,x2}
b) Means beautiful applicant with BS are {x1,x2}
c) Means brilliant applicant with SSCE are {x1,x2,x3,x4}
d) Means brilliant applicant with BS are {x1,x2}
e) Means brilliant applicant with MS are {x1,x2}
Tabular representation of soft set. (Table 1)
TOPSIS Method
“To solve multiple criteria decision-making problem Hwang and Yoon [10] introduced a technique, which is known as the TOPSIS method. He proposed a positive ideal solution and a negative ideal solution to support the shortest Euclidean distance. The basic assumption is that each criterion needs to be minimized or maximized. For ranking alternatives for closeness to the best answer, the TOPSIS is helpful. The process of TOPSIS is based on an optimum ideal solution since the maximum level is obtained by selecting the best alternative available. The ranking of an ideal solution is done in such a way that the best alternative has rank one while the worst alternative a rank approaching zero. For every alternative, there is an intermediate ranking between the best answer extremes. An identical set of choice criteria permits correct weighting of relative disease and therefore the optimum disease is alarming which needs attention. Here are presented the steps for the TOPSIS technique.
Step 1: Establishment of DM
First step in TOPSIS is to construct the decision matrix (DM) that is as follows
F : E → P (U )
Where l is the alternative index ( l =1, 2,..., q ); n is the number of potential sites and is the criteria index .
The elements R1, R2 ,..., Rq of the DM define the criteria while
A
Step 2: Calculation of the Normalized Decision Matrix
The normalized decision matrix (NDM) denotes the normalized values which represent the relative performance of the alternatives.
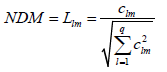
Step 3: Determination of the Weighted Normalized Decision Matrix
By multiplying every element of each column of normalized decision matrix got a weighted decision matrix.
V = Vlm = Wm x Llm
Step 4: Identification of the Positive Ideal Solution (PIS) and Negative Ideal Solution (NIS)
The PIS ( I + ) and the NIS ( I − ) are defined with respect to the weighted decision matrix as follows.
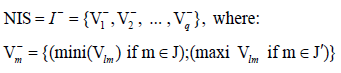
Where J ′ is associated with the non-beneficial attributes and J is associated with beneficial attributes.
Step 5: Separation Distance from PIS and NIS, of Each Alternative
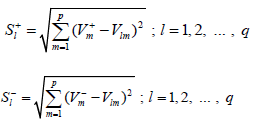
Where, l = Alternative index,
m = Criteria index.
Step 6: Relative Closeness to the Ideal Solution.
The relative closeness of the ideal solution is computed as
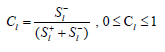
Step 7: Ranking of Preference Order
Ranking is done based on the values of l C the higher value of the relative closeness has a high rank and hence the better performance of the alternative. Rank the preference in descending order to compare the better performances of alternatives”.
A Decision-Making Method on Soft Set by TOPSIS
Soft set TOPSIS method
a) Step 1: Defining the problem
First, we define the set of decision-makers, set of candidates and set of parameters which are given as
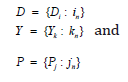
Then a soft set g over P is defined as
g: P→ Ῥ(Y)
b) Step 2: Construct the decision matrix for each decisionmaker
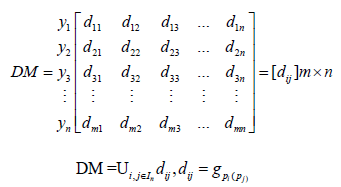
c) Step 3: Construct the weighted normalized decision matrix

And
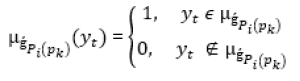
d) Step 4: Construct the decision matrix
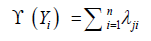
where ϒ (Yi) decide the values of yi, so the decision matrix is ii
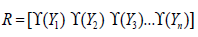
e) Step 5: Ranking the preference order
Ranking is done based on the values of ϒ (Yi) the higher the value of the relative closeness has high rank and hence the better performance of the candidates. Rank the preference in descending order to compare the better performances of candidates.
Application of soft set by TOPSIS method
a) Step 1
A bank manager wants to select two candidates out of from five which is our universal set
Y = {Y1, Y2, Y3, Y4, Y5}
Head office of the bank decide the parameters for the selection of candidates which are given here
P = {Qualification (Q), Tall (T), Beautiful (Be), Brilliant (Br) and Confidence (C)} and hire a team of five selectors (Decision makers) to choose two candidates out of five.
D = {D1, D2, D3, D4, D5}.
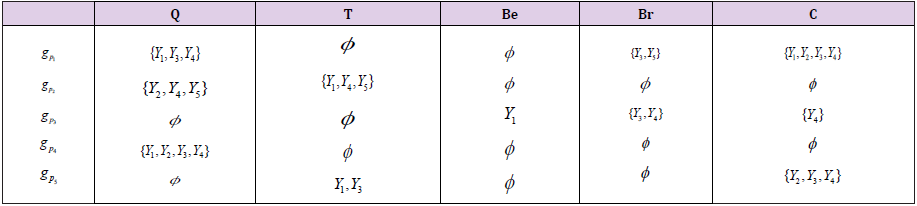
First, the first selector D1 chooses the set of parameters for the selection of candidates such as P1 = {Q, Br, C} and construct the soft set.
ǵP1= {(Q, {Y1, Y3, Y4}), (Br, {Y3, Y5}), (C, {Y1, Y2, Y3, Y4})}
Now, second selector D2 choose the set of parameters for the selection of candidates such as P2 = {Q, T} and construct the soft set.
ǵP2= {(Q, {Y2, Y4, Y5}), (T, {Y1, Y4, Y5})}
Now, third selector D3 choose the set of parameters for the selection of candidates such as P3 = {Be, Br, C} and construct the soft set.
ǵP3= {(Be, {Y1}), (Br, {Y3, Y4}), (C, {Y4})}
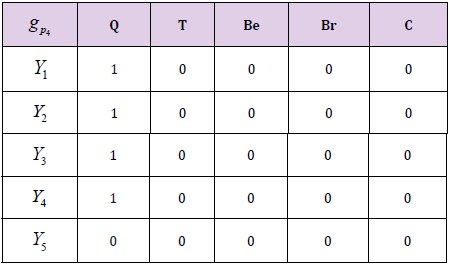
Fourth selector D4 choose the set of parameters for the selection of candidates such as P4 = {Q} and construct the soft set.
ǵP4= {(Q, {Y1, Y2, Y3, Y4})}
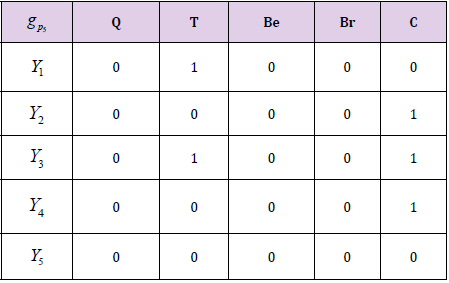
Finally, fifth selector D5 chooses the set of parameters for the selection of candidates such as P5 = {T, C} and construct the soft set.
ǵP5= {(T, {Y1, Y3}), (C, {Y2, Y3, Y4})}
b) Step 2
Now, we construct decision matrix for each selector where gpi represent the soft set. (Table 2)
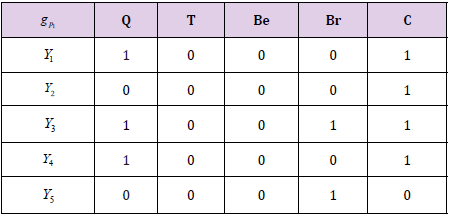
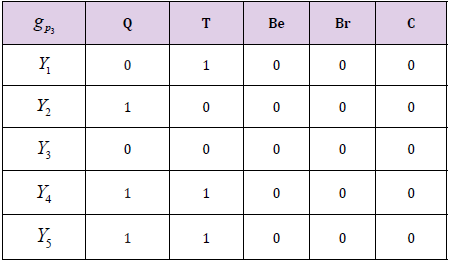
Now we construct the soft set for selectors Pi (Table 3) Then decision matrix is
Table 3: (A) Soft Set for Selector P1 (B) Soft Set for Selector P2 (C) Soft Set for Selector P3 (D) Soft Set for Selector P4 (E) Soft Set for Selector P5.
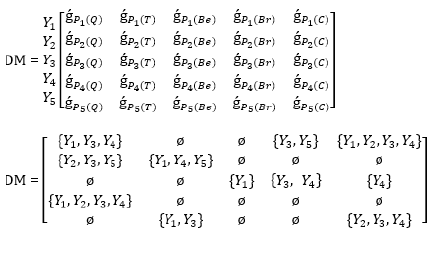
c) Step 3:
Construct weighted normalized decision matrix


So, the weight matrix is obtained as
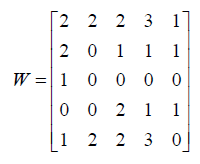
d) Step 4. Constructing the decision matrix (vector), R.
To find all elements of R individually
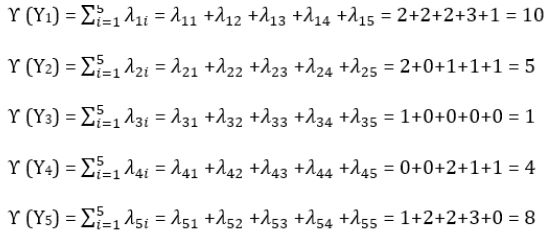
Thus, the DM of each candidate’s values for the decision-makers is obtained as
R= [10 5 1 4 8]
e) Step 5. Ranking the Preference Order.
Ranking among the candidates would be created in the order in descending order of the values ϒ (Yj) calculated in the fifth step. So, when the fifth step in the calculation of the evaluation of the candidate from small to large ϒ (Y1) ˃ ϒ (Y5) ˃ ϒ (Y2) ˃ ϒ (Y4) ˃ ϒ (Y3) the order form is realized in the form of ranking Y1 ˃ Y5 ˃ Y2 ˃ Y4 ˃ Y3. In other words, we can say that Y1 and Y5 are the best candidates for the bank job.
Conclusion
In this paper, we discuss the soft set and TOPSIS method along with some definitions and examples. Secondly, we discuss the soft set TOPSIS method. Finally, we apply the soft set TOPSIS method for the selection of two best candidates for the bank job.
References
- Zadeh LA (1965) Fuzzy sets. Journal of Information and Control 8(3): 338-353.
- Molodtsov DA (1999) Soft set theory-first result. Computers and Mathematics with Applications 37(4-5): 19-31.
- Maji PK, Roy AR, Biswas R (2001) Fuzzy soft sets. Journal of Fuzzy Mathematics 9(3): 589-602.
- Maji PK, Roy AR, Biswas R (2002) An application of soft sets in a decision-making problem. Computers and Mathematics with Applications 44(8-9): 1077-1083.
- Maji PK, Roy AR (2003) Soft set theory. Computers and Mathematics with Applications 45(4-5): 555-562.
- Chen D, Tsang ECC, Yeung DS, Wang X (2005) The parameterization reduction of soft sets and its applications. Computers & Mathematics with Applications 49(5-6): 757-763.
- Ali MI, Feng F, Liu XY, Min WK (2009) On some new operations in soft set theory. Computers and Mathematics with Applications 57(9): 1547-1553.
- Yeşim YA, Aytaç Y, Ahmet O (2012) Fuzzy TOPSIS Method in Supplier Selection and Application in the Garment Industry. Fibres and Textiles in Eastern Europe 20(4).
- GR Jahanshahloo, F Hosseinzadeh Lotfi, M Izadikhah (2006) Extension of the TOPSIS method for decision-making problems with fuzzy data. Applied Mathematics and Computation 181(2): 1544-1551.
- C Hwang, K Yoon (1981) Multiple Attribute Decision Making: Methods and Applications. In C Hwang, K Yoon (Eds.), (1st Edn), A State-of-the-Art Survey 1.
- SJJ Chen, CL Hwang (1992) Chapter 5 Fuzzy Multiple Attribute Decision Making Methods. Springer-Verlag Berlin Heidelberg 375: 289-486.
- CT Chen (2000) Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst 114(1): 1-9.
- A Awasthi, SS Chauhan, SK Goyal (2011) A multi-criteria decision-making approach for location planning for urban distribution centers under uncertainty. Math Comput Model 53 (1-2): 98-109.
- T C Chu (2002) Selecting plant location via a fuzzy TOPSIS approach. Int J Adv Manuf Techno 20(11): 859-864.
- D Yong (2005) Plant location selection based on fuzzy TOPSIS. Int J Adv Manuf Technol 28(7-8): 839-844.
- M Zulqarnain, M Saeed (2016) An application of Interval valued fuzzy soft matrix (IVFSM) in decision making. Sci Int (Lahore) 28(3): 2261-2264.
- M Zulqarnain, M Saeed (2016) Comparison between fuzzy soft matrix (FSM) and interval valued fuzzy soft matrix (IVFSM) in decision making. Sci Int (Lahore) 28(5): 4277-4283.
- M Zulqarnain, M Saeed (2017) A New Decision-Making Method on Interval Valued Fuzzy Soft Matrix (IVFSM). British Journal of Mathematics & Computer Science 20(5): 1-17.
- Selim Eraslana (2015) A Decision-Making Method via TOPSIS on Soft Sets. journal of new results in science 8: 57-71.
- M Zulqarnain, F Dayan, M Saeed (2018) TOPSIS Analysis for the Prediction of Diabetes Based on General Characteristics of Humans. International Journal of Pharmaceutical Sciences and Research 9(7): 2932-2939.

 Research Article
Research Article