Abstract

The thermal and thermodynamic calculations by using Gaussian 09 were carried out. The aim of this work is to evaluate the physical parameters necessary for solvation process and use them for the calculation of individual thermodynamic parameters which necessary for explaining solvent effect parameters in water. Beginning from the partition functions for the compound used, individual and statistical thermodynamic were calculated and their values were discussed.

Keywords: Glycine; Thermal; Thermodynamics Parameters; Partition Functions; Electronic Thermal Energy; Heat Capacity at Constant Volumes; Translational Energy; Rotation Energy; Vibration Energy

Abbreviations: DFT: Density Functional Theory; ZPVE: Zero-Point Vibrational Energy; CV: Constant Volume; GL: Glycine

Introduction

For accurate study, thermodynamic analysis is important for obtaining the individual and specific micro data to illustrate the solute-solvent interaction picture by using Gaussian 09 program. Density functional theory (DFT) were carried out on applying Gaussian 09 program packages [1]. The Beck’s 3- parameters exchange functional and Lee – Yang – Paar’s correlation functions (B3LYP) were studied in DFT method [2], 6-321G (D,P) basis sets were applied to give stable geometry. In Gaussian 09 the ideal gas approximation for non-interacting particles are used for starting calculations. The very important point for the calculations is the estimation of partition function Q (V,T) which correspond to total partition function [3,4]. The aim of the work is to complete the study of the active compound glycine thermochemical properties to get light on it and explain its solvent effect (Table 1).
The necessary equations used for evaluating entropy, energy, heat capacity resulting from the calculation frequencies for glycine in water by the use of Gaussian 09 package are given below:

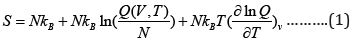
Where 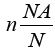and N_A k_B = R where N_A is Avogadro’s number R is the gas constant, k_B is Boltzmann’s constant and Q is the partition function changing into log scale we get:

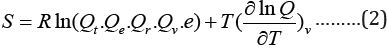
Where Q is the partition function (total ), the Q_t, Q_e, Q_r, Q_v, is the translational, electronic, rotational and vibrational partition function.

The thermal energy can also be obtained from the partition function:

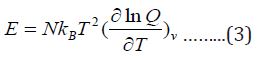
The heat capacity can be evaluated by applying equation4:

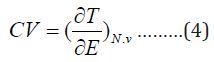
Equations above mentioned will be used for estimation of the available thermodynamic for inorganic and organic compounds from the given and evaluated partition functions [5-10]. The theoretical calculations were done from the contributions for the translation, rotational motion and electronic contributions. The data which obtained from frequency analysis by the need of partition function. For vibrational motion, we Choose the first vibrational energy K, level to be zero level, the corresponding partition function is expressed as [11].

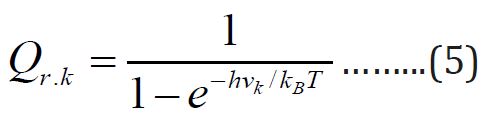
Where k_B is Baltzmann constant ( k_B= 1.38066 x10^-23 J/k), h is planck’s constant (h=6.626 x10^-23 J.S) h_vk / k_BT = Ɵ_v,k Is defined as vibrational frequency of mode k. The zero energy is defined as fully dissociated limit (free electrons and bore nuclei). At zero absolute temperature, there are very small motions of molecules, which is the zero-point vibrational energy (ZPVE or ZPE).
The zero-point vibrational energy ZPVE must be added to obtain all 3N-6 vibrational modes, the total ZPVE [11] is

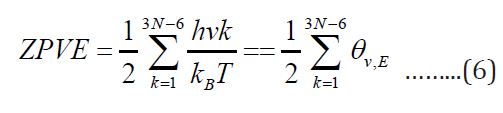
The ZPVE was calculated for glycine in water.

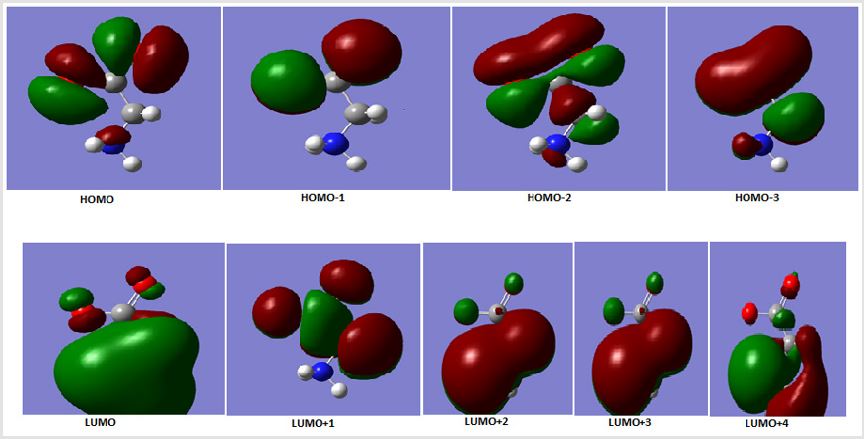
HOMO and LUMO Orbitals

The HOMO and LUMO orbitals are evaluated theoretically and drawn in Figure 1 indicating the last fill orbital shape and minimum empty orbital. These orbitals obtained from alpha orbitals evaluated from Gaussian 09 package. Also, different HOMO orbitals were represented in Figure 1 which are HOMO-1, HOMO-2, HOMO-3. HOMO as explained before in the last filled orbitals. Different loops was appeared in last HOMO orbital which is jointed in lower filled HOMO orbital. The LUMO orbital is bigger one in comparsion to the orbitals above it, like LUMO+1, LUMO+2, LUMO+3 and LUMO+4 (Figure 1). The energy gap which is the difference between last HOMO and first LUMO orbitals is 0.2294ev. This value indicate that glycine in water can conduct electricity in good case. The energy gap between last HOMO and other LUMO orbitals increase as represented in Table indicating less conduction for large transfer of electrons.
Different contribution for Glycine in Water:
The different types of motions were studied theoretically for glycine in water and summarized as given next.

Contributions from Translation

The translational partition function was used for evaluating the translational entropy (which donate e factor which comes from Stirling’s approximation:

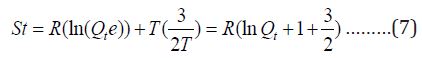
The contribution to internal energy is:

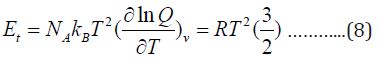
Finally, the heat capacity at constant volume is

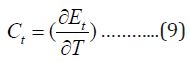
Contributions from Electronic Motion

This last contribution can be calculated from the electronic partition function

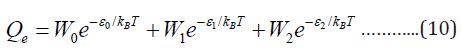
Where w is the degeneracy of energy level, E₀ E₁ E₂ E_n is the energy in n-level.
The entropy due to electronic kinetic motion is:

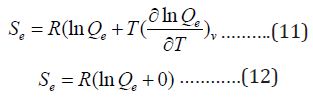
Since we have no temperature dependent terms in partition functions, the electronic heat capacity and electronic motion energy and internal energy are both zero

Contribution from Rotational Motion

The rotational partition function is:

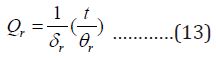
Where θ_r =h²/ 8 π² Ik_B I is the moment of inertia δ_r is the rotational diameter
The entropy of rotation is given by:

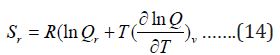
The contribution for rotation internal energy is:

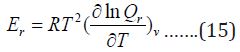
And contribution to heat capacity is:

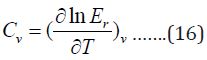
For nonlinear molecule as glycine, the rotation energy and heat capacity at constant volume is given by:

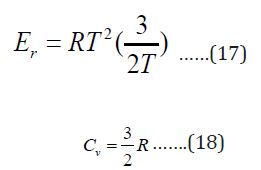
Contributions from Vibrational Motion

This last contribution follow equation (19)

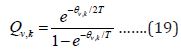
The total entropy, energy and Cv from vibrational partition function are:

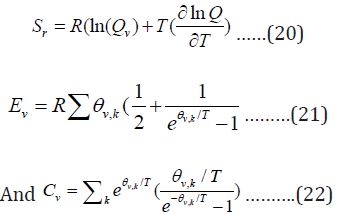
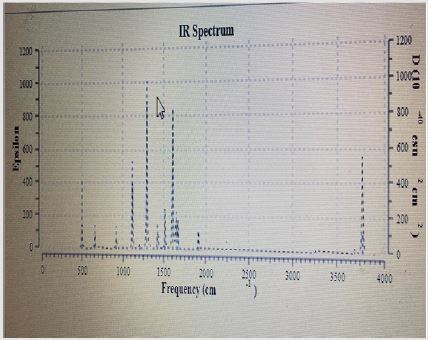
Output from Frequency Calculations. The first part of the obtained frequency data for glycine in water using theoretical evaluation by Gaussian 09 is the degree of freedom which is 15 for glycine in water. The rotation constant in GHZ are 10.588, 4.2511 and 3.149. The calculation based on standard basis 3-21G. The second result is the dipole moment and multiple moments for glycine in water. The individual different moment direction are given in Appendix table with high total dipole moment of 14.013 in water explaining it high activity in aqueous media. Glycine also has big quadrupole moment, traceless quadrupole moment, octupole moment and hexadecapolar moments as given in colligative table for Glycine properties. All different types of moments are calculated in Debye and using field-independent basis as done theoretically by the Gaussian package program Figure 1. The third output result is the infrared bands for Glycine in water which given in Figure…. This Figure contains at least 16 peak ranging from very weak to very sharp. The theoretical program gave 24 bands with three imaginary negative values for the different frequencies of stretching and bending in Glycine compound Figure 2. NMR calculated spectra gave the necessary peaks. The next part gives some characteristics of Glycine based on the moment of inertia including its energies values of 170.45, 424.52, and 573.02 atomic units as explained in colligative Figure 2.

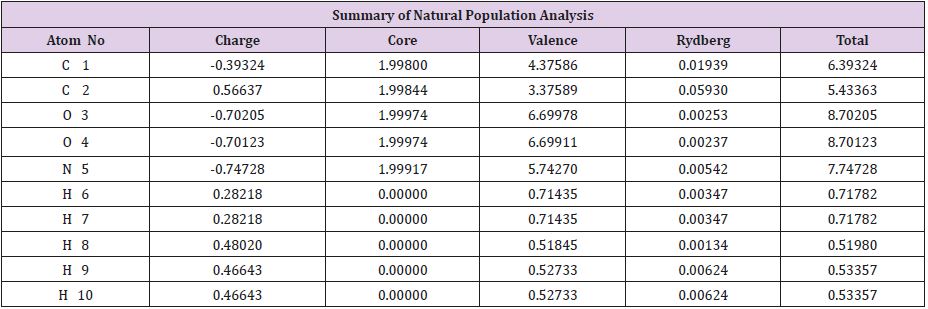
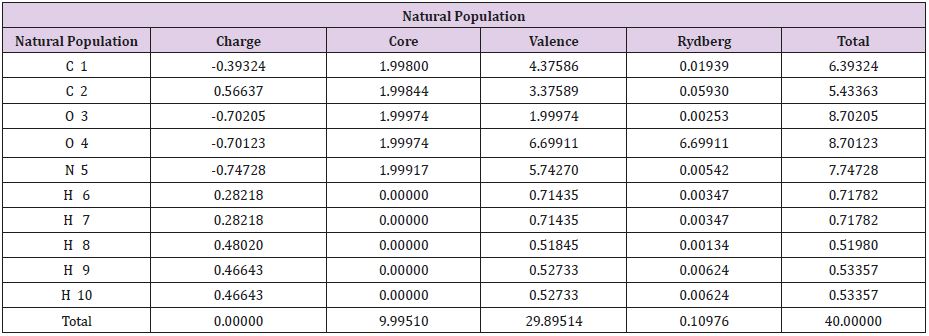
The zero-point energy is calculated using non-imaginary frequencies. Glycine molecule is an asymmetric top, rotational symmetry number is 1, rotational temperatures are 0.5081, 0.204 and 0.151 in kelvin, rotational constants are 76.55, 20.429in GHZ. The zero-point vibrational energy is 226.21 kJ/mol since all the thermochemistry and thermodynamic data depend on Glycine structure Table 2. All thermal and thermodynamic parameters evaluated include the zero-point energy, because the first line gives the correction to different types of energies. The next part in the colligative table listing different individual contributions to internal thermal energy (E_thermal), heat capacity at constant volume (CV) and entropy (S). For every low different frequency mode, there will lines label (vibration 1), (vibration 2) give contribution of the values estimated with source of error. Finally, table gives the different partition function. The line Bot for vibrational partition function with zero energy, V=0 computed with zero being first vibrational level, V=1, computed with first level being first vibrational level and so on. All thermodynamic and thermal properties calculated for glycine in water prove its high activity as very reactive agent. It is clear from Table…. for the NBO (Natural bonding orbitals) net charge zero and individual charges in each atom in the molecule (Table 3 and Figure 3).

Conclusion

All the thermal, classic thermodynamics, IR, NMR, statistical thermodynamic data for glycine in water were calculated using Gaussian 09 theoretically in water. The data proves the activity of glycine in water as very reactive agent. This behavior is illustrated from molecular orbitals and colligative specific properties of glycine in water.

References

• Frisch MJ (1998) Ganssian Inc, Pittsbagh PA, USA.
• Beche AD (1993) Demsity functional thermoedemistry III, the role of exact exchange. J. Chan. Plays 98: 5648.
• Me Quarrie DA (1999) Melecular Thermodynamics. University Science bolas.
• Voung DC (2001) Computational Chemistry. A John Wiely & Sons, New York, USA.
• Chandra AK, Uchimara T (2001) Hardness Profile:  A Critical Study. J Phys Chem A 105(14): 3578-3582.
• Kaatz P, Donley EA, Shelton DR (1998) A comparison of molecular hyperpolarizabilities from gas and liquid phase measurements. J Chem Phys 108: 849-855.
• Cheng LT, Tam W, Meredith GR, Rikken G, Marader SR, et al. (1991) Experimental investigations of organic molecular nonlinear optical polarizabilities. 2. A study of conjugation dependences. J Phys Chem 95(26): 10631-10643.
• Polvarapu PL (1997) Mol Phys 91: 551.
• Michael Bendihov, Ritzha Apeloig (2002) J Phys Chem 106: 4880-4885.
• Parr RG, Yang W (1989) Density - Functional theory of Atoms and Molecules. Oxford University Press, New York, USA.
• Koch W, Holthausen MC (2001) A chemist's guide to Density Functional Theory. Wiley - VCH: New York, USA.

Abstract

The thermal and thermodynamic calculations by using Gaussian 09 were carried out. The aim of this work is to evaluate the physical parameters necessary for solvation process and use them for the calculation of individual thermodynamic parameters which necessary for explaining solvent effect parameters in water. Beginning from the partition functions for the compound used, individual and statistical thermodynamic were calculated and their values were discussed.

Keywords: Glycine; Thermal; Thermodynamics Parameters; Partition Functions; Electronic Thermal Energy; Heat Capacity at Constant Volumes; Translational Energy; Rotation Energy; Vibration Energy

Abbreviations: DFT: Density Functional Theory; ZPVE: Zero-Point Vibrational Energy; CV: Constant Volume; GL: Glycine