Abstract
Purpose: To determine the coefficients of bi- and tri-exponential functions for the best fit of radial dose functions of the iodine brachytherapy source: 125I I-Seed AgX100.
Methods and Materials: The Particle Swarm Optimization (PSO) method was used to search for the coefficients of the bi- and tri-exponential functions that yield the best fit to data published for a few selected radial distances from the source. The coefficients were encoded into particles, and these particles ‘fly’ through the searching space in optimization by following their local and global best-known positions. In each generation, particles were evaluated through their fitness function and their positions were changed through their velocities. This procedure was repeated until the convergence criterion was met or the maximum generation was reached. All best particles were found in less than 1,500 generations.
Results: For the 125I I-seed AgX100 considered as a point source, the maximum deviation from the published data is less than 2.9% for bi-exponential fitting function and 0.2% for tri-exponential fitting function. For its line source, the maximum deviation is less than 1.1% for bi-exponential fitting function and 0.08% for tri-exponential fitting function.
Conclusion: PSO is a powerful method in searching coefficients for bi-exponential and tri-exponential fitting functions. The bi- and tri-exponential models of 125I I-seed AgX100 point and line sources obtained with PSO optimization provide accurate analytical forms of the radial dose function. The tri-exponential fitting function is more accurate than the bi-exponential function.
Keywords: Radial dose function; Brachytherapy; Radioactive seeds; Optimization; Fitting function; Particle swarm optimization
Introduction
Since Theragenics Corporation (Buford, GA) introduced their I-125 seed model AgX100 in 2010, several studies have been published either from experimental measurement or from theoretical calculation like Monte Carlo [1-5]. Polynomial functions and gradient-based optimization algorithm are usually used in searching the coefficients of its radial dose function [6]. In this study, a global optimization method-Particle Swarm Optimization (PSO) - was used to determine these coefficients. PSO was first proposed by Kennedy and Eberhart in 1995 and is a computer simulation of the social behavior of bird flocking, fish schooling and swarming theory [7]. According to this theory, individual member in the school have more chances to get food or avoid predators through information sharing among all other members in the school.
This social sharing of information is much more important than individual competition for food whenever the resource is scarce and unpredictably distributed in a large space. PSO is related to evolution computation, and especially to genetic algorithm and evolutionary programming. However, compared with the later two algorithms, PSO is much simpler and computationally less expensive [8-11]. Furthermore, like the other two methods, PSO does not require gradient calculation, so it can be used to solve problems involving non-differentiable functions as is required by traditional optimization methods. Many PSO variants have been published to improve the algorithm [12-15]. Some variants were used in radiotherapy treatment planning [14,15]. Li et al. 14 adopted PSO to automatically select beam angles by treating each beam configuration as a particle (possible candidate) and the beam intensity maps were optimized by a traditional conjugate gradient algorithm [16].
The particles were evaluated by using a physical objective function and evolved through cooperation and competition among themselves with time (generations). It shows PSO-based algorithm outperformed or at-least comparable to the genetic-algorithm in computation and robustness. A multi-objective PSO was also used to optimize beamlet intensities in the intensity-modulated treatment inversing planning [15]. Their preliminary work shows PSO has a very good convergence speed in the optimization procedure. In the current study, we applied PSO to determine the coefficients of bi- and tri-exponential functions to obtain an analytic expression for the radial dose functions of a radioactive seed: 125I I-seed AgX100 source.
Method and Materials
Bi- and tri-exponential fitting functions for the radial dose function g(r) can be expressed as16
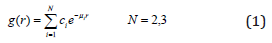
where ci and μi are the coefficients to be determined and r is the radial distance. The fitting coefficients in Eq. (1) were encoded into a particle which is defined as:
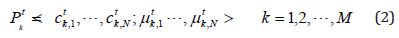
where M is the total number of the particle population and t is the generation index. The particle positions of the first generation are randomly selected and uniformly located in the searching space. In the following generations, each particle is updated through two ‘best’ values. The first value is the best position the particle has achieved so far – it is called ‘local’ best value:
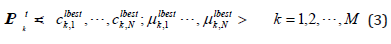
where LPtk is the best position of Particle k until iteration t. And the second-best value is the best solution achieved by any particle in the population – which is called ‘global’ best value:
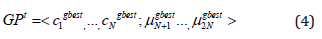
where GPt is the best position of any particle until iteration t. The varying velocity for any particle position can be expressed as:
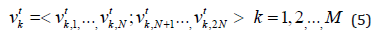
and it can be updated through the above two ‘best-so-far’ values:
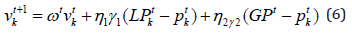
where ωt is the inertia weight which controls the amount of recurrence in the particle’s velocity? ωt is a linear variable defined as:
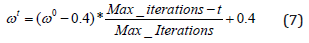
where ω0 is the initial inertia weight and was set to 0.9 in the current study. The ‘Max_iterations’ is the maximum number of iterations used to terminate the searching procedure. η1 and η2 in Equation (6) are the learning factors and γ1 and γ2 are random variables between 0 and 1. The new particle position can be updated as:
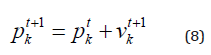
Figure 1 shows the concept of particle position updating procedure in the two dimensions. A fitness function is used to evaluate the ‘goodness’ of each particle. In our fitting process, the same fitness function was used as in our previous study14.
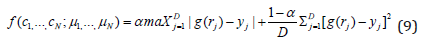
whereα is a weighting factor to balance the maximum difference (the first item on the right side) and the average difference (the second item). The value of α was set to 0.3 as before. In the above equation, j is the index number of radial distances rj. D is the total number of tabulated datum points for the source and yj is the expected data.
The particles are continually being updated through Eq. (6) to Eq. (8) until convergence (less than 10-6) or the maximum number of generations (1,500) is reached. A more detailed description of the PSO algorithm can be found elsewhere [7-9].
Results
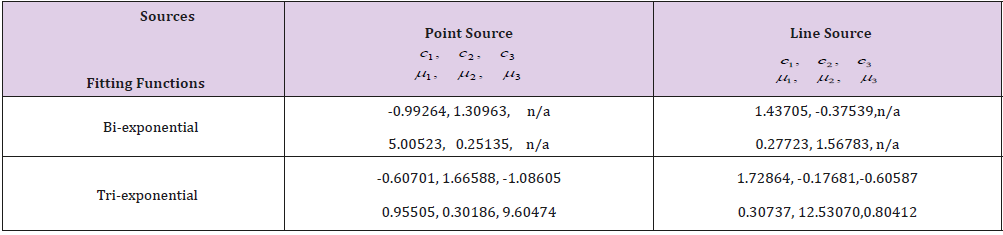
There are 21 tabulated radial distances for 125I I-seed AgX100 point source or line source 2. The population of particles was set to 50, and the maximum velocity was set to 100 for bi-exponential or tri- exponential fitting. The maximum ranges for these coefficients were set between -100 and 100. The learning factors (η1 and η2) were set to 2. After 1,500 generations, the best coefficients were determined. Table 1 shows the coefficients of bi- and tri-exponential fitting functions.
Table 1: Coefficients for the bi- and tri-exponential fitting functions of 125I I-seed AgX100 bracytherapy source.
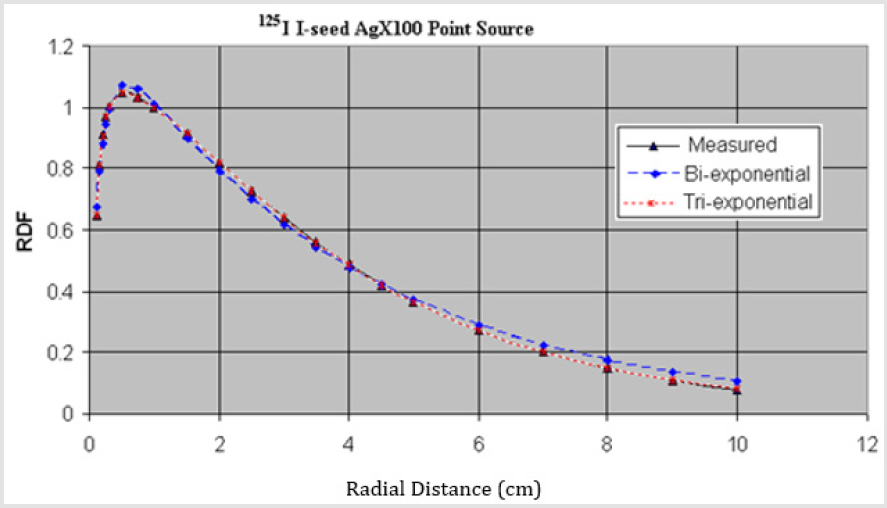
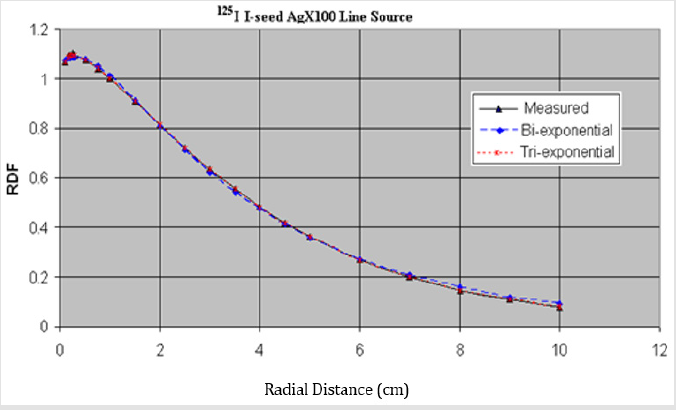
Figures 2 & 3 show the comparison between the measured data and the two fitting functions for the point source (Figure 2) and line source (Figure 3).
Figure 2: Comparison of bi- and tri-exponential fitting values with the measured data for the 125I I-seed AgX100 point source.
Figure 3: A comparison bi- and tri-exponential fitting values with the measured data for the 125I I-seed AgX100 line source.
For 125I I-seed AgX100 point source, the maximum deviation is less than 2.9% for bi-exponential fit and 0.2% for tri-exponential fit. For the line source, the maximum deviation is less than 1.1% for bi-exponential fit and 0.08% for tri-exponential fit.
Conclusion
PSO is a powerful optimization tool for finding the best fitting coefficients for bi- and tri-exponential fitting functions of the 125I I-seed AgX100 brachytherapy seeds. The bi- and tri-exponential models of line and point sources obtained with PSO optimization provide accurate analytical forms of the radial dose function. The triexponential fitting function agrees much better with the published data than the bi-exponential one. Compared to tedious table entries to characterize a seed, the entry of a relatively small number of fitting coefficients would greatly simplify the commissioning of treatment planning systems. Analytic fitting functions would also be beneficial in the development of institution-made quality-assurance software tools for independent verification of doses provided by commercial treatment planning systems. The close agreement with measured point dose suggests that the fitting functions may yield more accurate doses between points of measurement than straight linear interpolation.
References
- Chen Z, Bongiorni P, Nath R (2012) Experimental characterization of the dosimetric properties of a newly designed I-Seed model AgX100 125I interstitial brachytherapy source. Brachytherapy 11(6): 476-482.
- Mourtada F, Mikell J, Ibbott G (2012) Monte carlo calculations of AAPM task group report No. 43 dosimetry parameters for the (125) I I-Seed AgX100 source model. Brachytherapy 11(3): 237-244.
- Moutsatsos A, Pantelis E, Papagiannis P, Baltas D (2014) Experimental determination of the Task Group-43 dosimetric parameters of the new I25.S17plus 125I brachytherapy source. Brachytherapy 3(6): 618-626.
- Warrell GR, Xing Y, Podder TK, Traughber BJ, Ellis RJ (2018) Reduction of seed motion using a bio-absorbable polymer costing during permanent prostate brachytherapy using a mick applicator technique. J Appl Clin Med Phys 19(3): 44-51.
- Pagulayan C, Heng SM, Corde S (2019) Dosimetric validation of the Theragenics Agx-100®I-125 seed for ROPES eye plaque brachytherapy. Australas Phys Eng Sci Med 42(2): 599-609.
- Taylor RE, Rogers DW (2008) More accurate fitting of 125I and 103Pd radial dose functions. Med Phys 35(9): 4242-4250.
- Heppner F, Grenander U (1990) A stochastic nonlinear model for coordinated bird flocks. In The Ubiquity of Chaos (Edited by Krasner E), pp 233-238, AAAS Publications, Washington, DC, USA.
- Reynolds CW (1987) Flocks, herds and schools: A distributed behavioral model. Computer Graphics 21(4): 25-34.
- Eberhart RC, Kennedy J (1995) A new optimizer using particle swarm theory. Proceedings of the Sixth International Symposium on Micromachine and Human Science, Nagoya, Japan. p. 39-43.
- Eberhart RC, Shi Y (1998) Comparison between genetic algorithms and particle swarm optimization. Evolutionary Programming VII: Proceedings of the Seventh Annual Conference on Evolutionary Programming, San Diego, 1447: 611-616, CA.
- Poli R, Kennedy J, Blackwell T (2007) Particle swarm optimization. An overview. Swarm Intelligence 1(1): 33-57.
- Chun-Feng W, Kui L (2016) A Novel Particle Swarm Optimization Algorithm for Global Optimization, Computational Intelligence and Neurosci.
- Naresh M, Sarma TH (2018) A Tunable Particle Swarm Size Optimization Algorithm for Feature Selection, Published in IEEE Congress on Evolutionary Computation (CEC).
- Li Y, Yao D, Yao J, Chen W (2005) A particle swarm optimization algorithm for beam angle selection in intensity-modulated radiotherapy planning. Phys Med Biol 50(15): 3491-3514.
- Li G, Cao D (2010) A multi-objective particle swarm algorithm for the optimization of IMRT inverse planning, In 2010 3rd International confe Biomed Eng informatics pp. 1327-1330.
- Wu X, Brezovich I, Fiveash J (2009) Bi- and tri-exponential fitting to TG-43 radial dose function of brachytherapy sources based on a genetic algorithm. Brachytherapy (8): 361-366.

 Short Communication
Short Communication