Abstract
In this work we received the stationary set of the control system of the hysteresis deformation of the electro magneto elastic actuator in form the segment of the straight line. The aim of this work is to determine the condition of the absolute stability on the derivative for control system of the deformation of the electro magneto elastic actuator for nano biomedicine. We used the frequency methods for Lyapunov stable control system to calculate the absolute stability of the control system with electro magnetoelastic actuator. In result we determined the condition of the absolute stability on the derivative for the control system with the electro magneto elastic actuator for nano biomedicine.
Keywords: Condition Absolute Stability; Control System; Electro Magneto Elastic Actuator; Piezo Actuator; Hysteresis and Butterfly Characteristics; Stationary Set; Transfer Function
Introduction
In this work the condition of the absolute stability on the derivative for control system of the deformation of the electro magneto elastic actuator is calculated. The control systems with electro magneto elastic actuator on piezoelectric, electrostrictive and magnetostrictive effects solves problems of the precise matching in the nano biomedicine, the compensation of the temperature and gravitational deformations of the equipment, the wave front correction in the adaptive laser system [1-14]. The piezo actuator for nano biomedicine is used in the scanning tunneling microscope, the scanning force microscope, the atomic force microscope, in the gene manipulator [15-29]. The problems of using criteria absolute stability of the control system with electro magneto elastic actuator for nano biomedicine are discussed. The stationary set of the control system of the deformation of the electro magneto elastic actuator is received.
Condition Absolute Stability Control System
The electro magneto elastic actuator on piezoelectric, electrostrictive or magnetostrictive effects is used in the control systems for the micro and nano surgical repairs, the micro and nano robotics, the micro and nano manipulators and injectors for nano biomedicine [1-6]. The aim of this work is to calculate the condition of the absolute stability on the derivative for control system of the deformation of the electro magneto elastic actuator for nano biomedicine. The frequency methods for Lyapunov stable control system are used to determine the condition of the absolute stability of control system [2] with electro magneto elastic actuator for nano biomedicine.
We received the sufficient condition absolute stability control system with the hysteresis nonlinearity of the electro magneto elastic actuator using the Yankelovich absolute stability criterion with the condition on the derivative. This criterion is the development of the Popov absolute stability criterion [2]. For the Lyapunov stable control system and the Yalubovich absolute stability criterion for the systems with the single hysteresis nonlinearity provides the simplest and pictorial representation of results of the investigation of the stability of the strain control system with the electro magneto elastic actuator for nano biomedicine. For description of the control system we use the transfer function of the linear part of the system Wij(P) and the hysteresis function of the relative deformation Sj of the electro magneto elastic actuator [16]. We have the hysteresis characteristic of the electro magneto elastic actuator in the following form
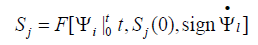
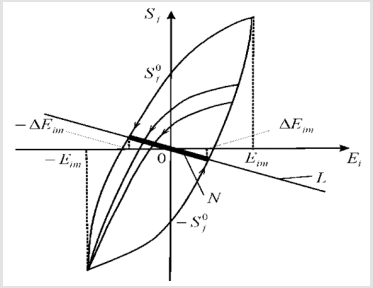
where Sj is the relative displacement of the cross section of the actuator along j axis, Ψi is the control parameter of the actuator along i axis. The hysteresis function Sj at each time instant t depends on the behavior of the function Ψi=Ei or Ψi=Hi, where Ei and Hi are the electric field strength and the magnetic field strength on the interval [0,t], the value of t, the initial value Sj (0), and the sign of the rate Ψ ̇i of the field strength variation. Let us consider hysteresis type characteristic of the deformation of the electro magnetoelastic actuator for Nano biomedicine on Figure 1.
The set Sj(0) is the vertical segment [S0j, -S0j ] bound by the points of intersection of the ordinate axis with the hysteresis loop at the maximum admissible field strength in the actuator. Therefore, we receive the stationary set for the deformation of the piezo actuator on Figure 1 for the stable linear part of the control system, where the equation for the straight-line L has the form
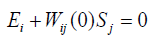
In static regime we have the value of the transfer function Wij(0) of the linear part of the control system for the deformation of the piezo actuator. The set of points N’s for intersection of this straightline L with the hysteresis characteristic represents the segment of the straight line marked on Figure 1. At Ei0=E0(0) and Sj0=Sj(0) we have the stationary solution to the control system with hysteresis. The stationary set N of the system is the marked segment of straight-line L in Figure 1 with the set of pairs (Ei0, Sj0). Each point of intersection of the hysteresis nonlinearity with the partial loops and the straight-line L corresponds to one equilibrium position with the coordinates (Ei0, Sj0). Therefore, for the stationary set the equation has the following form
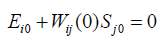
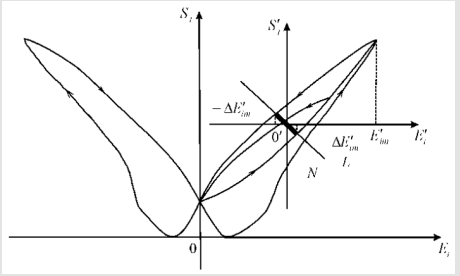
Let us consider butterfly type characteristic of the deformation of the electro magneto elastic actuator for nano biomedicine. For the actuator with the electrostrictive effect the deformation characteristic on butterfly wings is observed for unipolar change of the electric field strength on Figure 2.
The particular cycle on one wing of butterfly is the hysteresis loop. For butterfly type characteristic deformation of actuator in the control system the coordinate origin is moved to new zero with top dash on Figure 2. For hysteresis loop on butterfly type characteristic we have stationary set N of the system marked segment of straight-line L in Figure 2. For the magnetostrictive actuator the deformation characteristic has the butterfly type. We have the continuous function Sj(Ei) of the hysteresis loop of the piezo actuator with the quantities of the derivative.
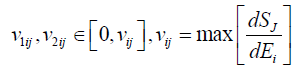
where the quantities of the derivative and are calculated using the hysteresis characteristic on Figure 1 for the maximum admissible electric field strength in the piezo actuator. The quantities 𝒱1ij=0 and 𝒱2ij=𝒱ij are the minimum and the maximum values of the tangent of the inclination angle of the tangent line to the hysteresis nonlinearity of the piezoactuator. Thus, we obtain
𝒱33: 𝒱31: 𝒱35= 𝒹33: 𝒹31: 𝒹15
where the ratios of the tangents of the inclination angle of the tangent line to the hysteresis nonlinearity of the piezo actuator for longitudinal, transverse and shift piezo effects are proportional to the ratios of the piezo modules. We have the expression for the sufficient absolute stability condition of the system with the hysteresis nonlinearity of the electro magneto elastic actuator using the Yakubovich absolute stability criterion with the condition on the derivative. The Yalubovich criterion is the development of the Popov absolute stability criterion [2]. For the Lyapunov stabile control system the Yalubovich absolute stability criterion for the system with the single hysteresis nonlinearity provides the simplest and pictorial representation of results of the investigation of the stability control system. The sufficient absolute stability condition of the control system of the deformation of the electro magneto elastic actuator at 𝒱1ij =0 and 𝒱2ij=𝒱ij have the form
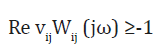
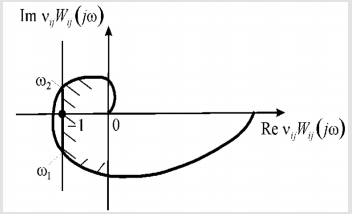
Where vijWij(jω) is the amplitude-phase characteristic of the open-loop system and in brackets j is the imaginary unity and ω is the frequency. The amplitude-phase characteristic of the open-loop system vijWij(jω) on Figure 3 should be situated to the right of the straight line
Re vijWij(jω)=-1
for all values of ω≥0.
Figure 3: Absolute stability criterion for control system with electro magneto elastic actuator, shaded corrected characteristic.
On the plane of the logarithmic amplitude frequency characteristic and the phase frequency characteristic for the absolute stability criterion the control system with electro magneto elastic actuator we have
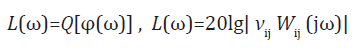
We have the corrected logarithmic amplitude frequency characteristic below the boundary curve in the form
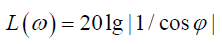
For the piezo actuator from PZT we received the value of the maximum tangent of the inclination angle of the tangent line to hysteresis nonlinearity about 1nm/V for longitudinal piezo effect and about 0.6nm/V for transverse piezo effect. We used the frequency methods for Lyapunov stable control system to calculate the condition the absolute stability of the control system with electro magneto elastic actuator for nano biomedicine.
Conclusion
We received the stationary set of the control system of the deformation of the electro magneto elastic actuator. The stationary set of the system is the segment of straight line for hysteresis or butterfly characteristic deformation of the actuator. We determined condition of the absolute stability on the derivative for the control system with the electro magneto elastic actuator for nano biomedicine.
Acknowledgement
None.
Conflict of Interest
No conflict of interest.
References
- Schultz J, Ueda J, Asada H (2017) Cellular actuators. Oxford: Butterworth-Heinemann Publisher, UK, pp.382.
- Yakubovich VA (2002) Popov's method and its subsequent development. European Journal of Control 8(3): 200-208.
- Zhou S, Yao Z (2014) Design and optimization of a modal-independent linear ultrasonic motor. IEEE Transaction on Ultrasonic, Ferroelectrics, and Frequency Control 61(3): 535-546.
- Przybylski J (2015) Static and dynamic analysis of a flex tensional transducer with an axial piezoelectric actuation. Engineering Structures 84: 140-151.
- Ueda J, Secord T, Asada HH (2010) Large effective-strain piezoelectric actuators using nested cellular architecture with exponential strain amplification mechanisms. IEEE/ASME Transactions on Mechatronics 15(5): 770-782.
- Karpelson M, Wei GY, Wood RJ (2012) Driving high voltage piezoelectric actuators in micro robotic applications. Sensors and Actuators A: Physical 176: 78-89.
- Afonin SM (2015) Block diagrams of a multilayer piezoelectric motor for nano and micro displacements based on the transverse piezo effect. Journal of Computer and Systems Sciences International 54(3): 424-439.
- Afonin SM (2008) Structural parametric model of a piezoelectric Nano displacement transducer. DoKlady Physics 53(3): 137-143.
- Afonin SM (2006) Solution of the wave equation for the control of an electromagnetic elastic transducer. Doklady Mathematics 73(2): 307-313.
- Cady WG (1946) Piezoelectricity: An introduction to the theory and applications of electromechanical phenomena in crystals. McGraw-Hill Book Company, New York, London pp. 806.
- Mason W (1964) Physical acoustics: Principles and methods. Vol.1. Part A. Methods and devices. Academic Press, New York, USA, pp. 515.
- Zwillinger D (1989) Handbook of differential equations, Academic Press, Boston, USA, p. 673.
- Afonin SM (2015) Structural-parametric model and transfer functions of electro elastic actuator for nano- and microdisplacement. Chapter 9 in Piezoelectrics and nanomaterials: Fundamentals, developments and applications. Parinov IA (Eds.), Nova Science, New York, USA, pp. 225-242.
- Afonin SM (2017) A structural-parametric model of electroelastic actuator for nano and microdisplacement of mechatronic system. Chapter 8 in Advances in nanotechnology. Bartul Z, Trenor J (Eds.), Nova Science, New York, USA, 19: 259-284.
- Afonin SM (2012) Nano and micro-scale piezomotors. Russian Engineering Research 32(7): 519-522,
- Afonin SM (2007) Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers. Mechanics of Solids 42(1): 43-49.
- Afonin SM (2017) Structural-parametric model electro magnetoelastic actuator Nano displacement for mechatronics. International Journal of Physics 5(1): 9-15.
- Afonin SM (2017) Structural-parametric model of piezo actuator nano and micro displacement for nanoscience. AASCIT Journal of Nanoscience 3(3): 12-18.
- Afonin SM (2016) Solution wave equation and parametric structural schematic diagrams of electro magnetoelastic actuators nano- and micro displacement. International Journal of Mathematical Analysis and Applications 3(4): 31-38.
- Afonin SM (2018) Structural-parametric model of electro magnetoelastic actuator for nanomechanics. Actuators 7(1): 1-9
- Afonin SM (2016) Structural-parametric models and transfer functions of electro magnetoelastic actuators nano and micro displacement for mechatronic systems. International Journal of Theoretical and Applied Mathematics 2(2): 52-59.
- Afonin SM (2017) Parametric block diagrams of a multi-layer piezoelectric transducer of nano- and micro displacements under transverse piezoelectric effect. Mechanics of Solids 52(1): 81-94.
- Afonin SM (2018) Structural parametric model of electro elastic actuator for nanotechnology and biotechnology. Journal of Pharmacy and Pharmaceutics 5(1): 8-12.
- Afonin SM (2019) A structural-parametric model of a multilayer electroelastic actuator for mechatronics and nanotechnology. Chapter 7 in Advances in nanotechnology. Volume 22. Bartul Z, Trenor J, (Eds.), New York: Nova Science: 169-186.
- Afonin SM (2019) Structural-parametric model and diagram of a multilayer electro magnetoelastic actuator for nanomechanics. Actuators 8(3): 1-14.
- Afonin SM (2018) Electro magnetoelastic actuator for Nano mechanics. Global Journal of Research in Engineering A: Mechanical and Mechanics Engineering 18(2): 19-23.
- Afonin SM (2019) Structural-parametric model multilayer electro magnetoelastic actuator nanodisplacement for nanomechatronics. International Journal of Physics 7(2): 50-57.
- Afonin SM (2019) Actuator for nano biomedical research. Biomedical Journal of Scientific and Technical Research 19(3): 14300-14302.
- Bhushan B (2004) Springer Handbook of Nanotechnology. Springer, Berlin, New York, USA, pp. 1222.

 Short Communication
Short Communication