Mini ReviewAbstract
Based on the general principles of the theory of electromagnetic radiation, bound to charged particles, it is shown that any living biological object emits electromagnetic waves of a certain intensity and power induced by the movement of red blood cells by curves. Noted, a what If for standard electromagnetic radiation take intensity healthy body, the when any violations functional abilities what or internal bodies always can fix local deviation radiated intensity from reference values, such way, install probable place disease.
Keywords: Curvilinear Trajectory; Electromagnetic Radiation; Electric Charge of Erythrocytes; Power of Radiation of Biological Object
Mini-Review
The question, which is devoted to the real work, has its rather long history, which dates back to the times of the last century, when closely began to deal with various incomprehensible phenomena such as moving objects without an explicit external Impact. In our recently published work [1] Was given a detailed mathematical solution to the problem of synchronization of two complanar physical pendulums, in which from a purely physical point of view it was strictly proved that the nature of this interesting phenomenon is purely electromagnetic in nature, and It is connected with the radiating ability of the pendency, and, as it turned out, it is absolutely unimportant whether they are metallic or made of plastic or even wooden.
In order to present the essence of this article we will use the basic principles and ideas of work [1], and we will represent a living organism, simulating it simply as a physical body within which streams of charged particles (erythrocytes) move. As is known [2], when the charges are moving with some variable speed v, they create a distance r non-stationary and spatially-heterogeneous electromagnetic field. Next we are will abbreviated characterize it acronym EM. It should be emphasized, however, that due to the far action characters of the EM field, the distance is not limited. Corresponding EM fields are connected with electric potential φ =φ (r,t) and magnetic A = A(r,t) simple linear rations, such as the [2]
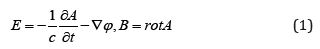
where E- is the electric field tension, B- is magnetic induction vector.
In the present case, that is, in the case of moving charges, in a real environment these potentials can be represented by the following symmetrical expressions [1]
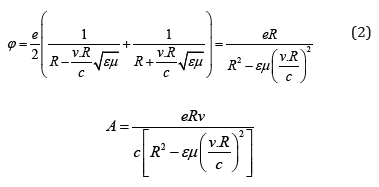
where e- is the particle charge, c- is a speed of light in a
vacuum, ε- is the dielectric permeability of the substance, and μ- is
magnetic permeability,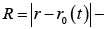 
is a distance from charge to observation point, r- is point of observation, is a trajectory of
the moving charge. If you introduce the average concentration of
red blood cells n, by analogy with the work [1] for the respective
potentials will have
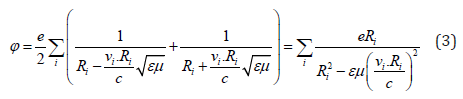
where the number characterizes the appropriate organ on which the blood flow moves.
Rations (3) tell us that the intensity of radiation, which is known [2], proportional to the square of the derivative of the velocity of the charged particle in time, should be characterized by an electric field of radiation generated by a moving charge, which according to (1) can be found as
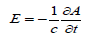
and according to (3) will be
Therefore, the total intensity of the radiation will amount
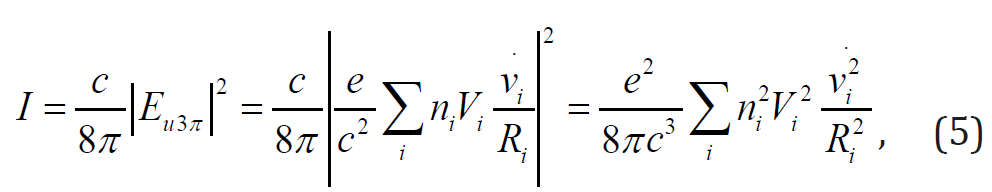
Where we believe that by virtue of the independence of diverse terms, only the squares of the corresponding values are left under the sign of the sum (like calculation of intensity at interference of EM waves). By and large this result is easy to understand, if we consider that the movement of blood, say, in the kidneys does not correlate with its movement, for example, in the liver or in the spleen. When the correlation between all organs is taken into account, the expression (5) will no longer be so compact. In this communication we will not be interested in such correlation.
Thus, the total biological power of the whole organism, which is obliged to the movement of red blood cells, should be defined as
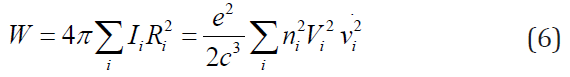
To assess the magnitude of the figure, it should be remembered that blood is a hydrodynamic flow on the capillaries and vessels of the body, and therefore can be described within the equation of Navier-Stokes. Indeed, according to for example (3) we have
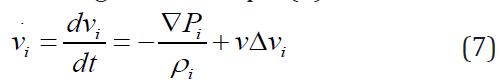
Where Pi- is a pressure inside i- body, ρi- is blood density in this i- th body, v- is kinematic viscosity? Ignoring the last term in the right part of the equation (7), we find the connection that interests us
Substituting (8) in the expression (6) for the full power of radiation we get as a result
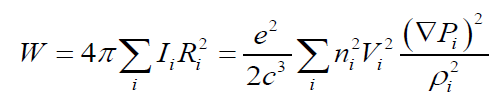
Since the same density can be imagined as, ρi=mni where m- is the mass of the local charged area of erythrocytes (that is, a small part of the whole mass of erythrocytes), come to the next remarkable formula, describing the full radiation of the entire body
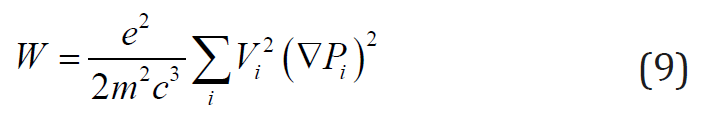
Note that the volume in this formula Vi can be considered known, which is not yet possible to assert about the pressure gradient. To estimate this, we use the following general physical considerations. Indeed, because blood flows through each organ, the necessary condition for its movement on it is the differential pressure at the inlet P2i and P1i outlet. This means that if the linear dimension iorgan there Li, the absolute value of the pressure gradient can be presented in the form of the next estimated ratio
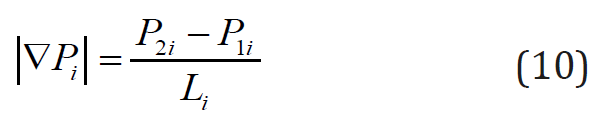
If you substitute now (10) in the general formula (9), we find the result
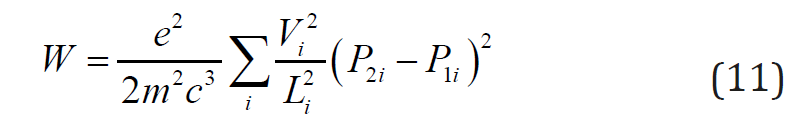
It should be said that in order of magnitude the pressure in any of our organs should be roughly equal to that of arterial, which can be denoted as P. The differential pressures at the inlet and outlet should be of the same order, because otherwise the blood would just stand still. This means that for any organ we can assume, first, that
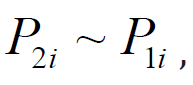
and, secondly, to believe that
Therefore, the expression (11) is even more simplified, and we get the following formula for estimating the power of radiation
The formula (13) responds to the question posed at the beginning of the article on the power of radiation characterizing any living organism, the origin of which is associated only with the radiation, going from red blood cells. According to (13) it can be easily appreciated. As to the general EM background of the biological body, it is characterized as known by the usual thermal radiation, and is described by the formula
where σ- is the Stefan-Boltzmann’s constant, T- is a temperature? It is clear that full radiation should be defined as the sum of
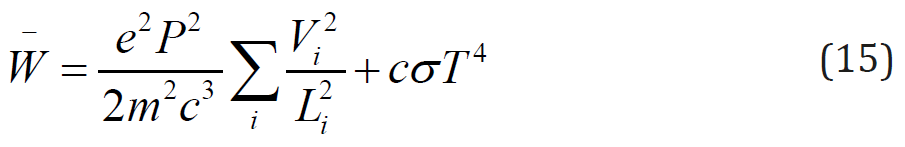
To quantify the radiation (13), we need to set the appropriate parameters. ~
We will assume that the charge of erythrocyte is e ~ 1018CTC (this
value is taken by us, based only on general physical considerations,
because in the reference books on medicine we simply did not find
it), and in order of magnitude we put pressure equal P ~ 104 Pa .
The mass of the local charged area of red blood cells may be, for
example, m ~ 10−15 g Speed of light 
The average linear size
of each organ, based simply on purely assessment considerations,
will be considered the same and we assume that Li ~ 10cm. Finally,
the total number of all the main organs of our body we will accept
equal to one hundred.
As a result of substitution of the given purely estimation numerical values in the general formula (13) цe immediately find
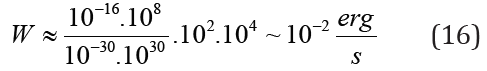
If the erg/s is transferred to watts, it will be approximately 10−9Watt. As we can see, the value of radiation power is quite small, but it clearly indicates the possibility of its fixation with the help of EM radiation detectors.
The noted fact allows us to easily estimate EM radiation, which is obliged to the charged particles of an organism which is an inherent property of any biological object.
Conclusion
In conclusion of the article we note a number of important
points.
1. It is shown that the power of radiation of charged particles
of an organism makes a comparatively small amount of order
10−9Watt.
2. At any painful manifestations the power should be less
than this reference.
3. The exact value of the radiation power can only be found
through the experiment.
References
- Gladkov SO, Bogdanova SB (2018) Chaotic dynamic of interacting pendulums. Mechanics, Material Science and Engineering 19: 1-9.
- Landau LD, Lifshitz EM (2004) Field theory. M Science.
- Landau LD, Lifshitz EM (2004) Hydrodynamics. M Science.
