Abstract

In this work, we obtain the parameters of the actuator for nano biomedical research. We have mathematical model of the actuator with the piezoelectric or magneto strictive effect.

Keywords: Piezoelectric actuator, Magneto strictive actuator, Electromechanics, Parameter.

Introduction

Actuator for nano biomedical research is used to nanomanipulations in the scanning microscope, the nanoliter pump, the gene manipulator, the cell penetration tool, the microsurgery [1−16]. We obtain the transfer functions and the characteristics of the actuators on the piezoelectric and magneto strictive effect for control system of the nano deformation for nano biomedical research [17−28].

Transfer function

The equation of electromechanics [8, 11] for relative deformation S_i of the piezoelectric or magneto strictive actuator has the form

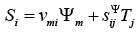
where 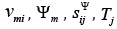are the module, the control parameter, the elastic compliance and the mechanical stress, and i, j,m are the indexes. We have the second order differential equation [8, 12, 14] for the actuator in the form

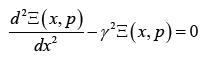
and the transfer function W( p) of the actuator

W( p) = Ξ( p) / Ψ( p)

where Ξ(p) ,Ψ( p) are transforms of Laplace the displacement and the control parameter, p, γ , x are the conversion parameter, the propagation coefficient, the coordinate.

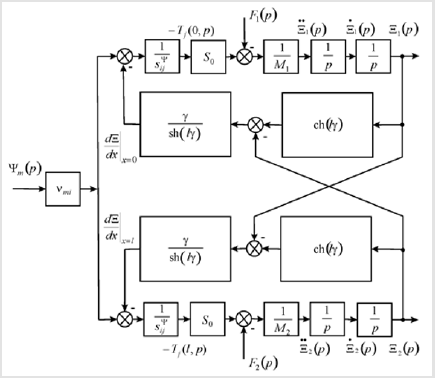
We drew model of the actuator from decision the equation of electromechanics and the second order differential equation [12- 15]. In result we have the mathematical model and the scheme of the actuator for nano biomedical research on Figure 1 with the piezoelectric or magneto strictive effect in the form

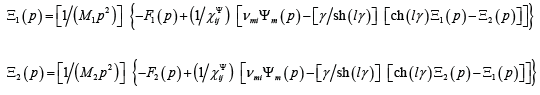
where Ξ¹ (p), Ξ² (p), F¹( p), F²( p) are transforms of the displacements and the forces of the faces, M₁, M₂, l are the mass and the length.

We receive the transfer function of the transverse piezoelectric actuator in the form

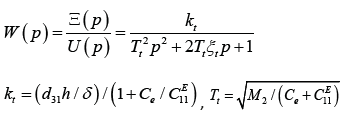
At d₃₁ = 2∙10^-10 m/V, h /δ = 20, U = 50 V, M₂ = 4 kg, C₁₁^E = 2∙10⁷ N/m, C_e = 0.5∙10⁷ N/m we obtain the parameters of actuator k_t = 3.2 nm/V, ξ₂ (∞) = 160 nm, T_t = 0.4∙10^-3 s.

Figure 1: Structural scheme of actuator for nano biomedical research.

Conclusion

In this work, we receive the transfer functions and the parameters of the actuator for the control system of the nano deformation for nano biomedical research. We obtain the mathematical model of the actuator from decision the equation of electromechanics and the second order differential equation.

References

• Schultz J, Ueda J, Asada H (2017) Cellular Actuators. Butterworth- Heinemann Publisher, Oxford, p. 382.
• Afonin SM (2006) Absolute stability conditions for a system controlling the deformation of an elecromagnetoelastic transduser. Doklady mathematics 74(3): 943-948.
• Zhou S, Yao Z (2014) Design and optimization of a modal-independent linear ultrasonic motor. IEEE transaction on ultrasonics, ferroelectrics, and frequency control 61(3): 535-546.
• Przybylski J (2015) Static and dynamic analysis of a flextensional transducer with an axial piezoelectric actuation. Engineering structures 84: 140-151.
• Ueda J, Secord T, Asada HH (2010) Large effective-strain piezoelectric actuators using nested cellular architecture with exponential strain amplification mechanisms. IEEE/ASME Transactions on Mechatronics 15(5): 770-782.
• Karpelson M, Wei GY, Wood RJ (2012) Driving high voltage piezoelectric actuators in microrobotic applications. Sensors and Actuators A: Physical 176: 78-89.
• Afonin SM (2015) Block diagrams of a multilayer piezoelectric motor for nano- and microdisplacements based on the transverse piezoeffect. Journal of computer and systems sciences international 54(3): 424-439.
• Afonin SM (2008) Structural parametric model of a piezoelectric nanodisplacement transduser. Doklady physics 53(3): 137-143.
• Afonin SM (2006) Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady mathematics 73(2): 307-313.
• Cady WG (1946) Piezoelectricity: An introduction to the theory and applications of electromechancial phenomena in crystals. McGraw-Hill Book Company, New York, London p. 806.
• Mason W (1964) Physical Acoustics: Principles and Methods. Vol.1. Part A. Methods and Devices. Academic Press, New York p. 515.
• Zwillinger D (1989) Handbook of Differential Equations. Academic Press, Boston p. 673
• Afonin SM (2015) Structural-parametric model and transfer functions of electroelastic actuator for nano- and microdisplacement. Chapter 9 in Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications. Ed. Parinov IA. Nova Science, New York pp. 225-242.
• Afonin SM (2017) A structural-parametric model of electroelastic actuator for nano- and microdisplacement of mechatronic system. Chapter 8 in Advances in nanotechnology. Volume 19. Eds. Bartul Z, Trenor J, Nova Science, New York pp. 259-284.
• Afonin SM (2012) Nano- and micro-scale piezomotors. Russian engineering research 32(7-8): 519-522.
• Afonin SM (2007) Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers.” Mechanics of solids 42(1): 43-49.
• Afonin SM (2014) Stability of strain control systems of nano-and micro displacement piezotransducers. Mechanics of solids 49(2): 196-207.
• Afonin SM (2017) Structural-parametric model electro magnetoelastic actuator nano displacement for mechatronics. International Journal of Physics 5(1): 9-15.
• Afonin SM (2017) Structural-parametric model of piezo actuator nanoand micro displacement for nanoscience. AASCIT Journal of Nanoscience 3(3): 12-18.
• Afonin SM (2016) Solution wave equation and parametric structural schematic diagrams of electro magnetoelastic actuators nano- and micro displacement. International Journal of Mathematical Analysis and Applications 3(4): 31-38.
• Afonin SM (2018) Structural-parametric model of electro magnetoelastic actuator for nano mechanics. Actuators 7(1): 1-9.
• Afonin SM (2016) Structural-parametric models and transfer functions of electro magnetoelastic actuators nano- and micro displacement for mechatronic systems. International Journal of Theoretical and Applied Mathematics 2(2): 52-59.
• Afonin SM (2017) Parametric block diagrams of a multi-layer piezoelectric transducer of nano- and micro displacements under transverse piezoelectric effect. Mechanics of Solids 52(1): 81-94.
• Afonin SM (2018) Multilayer electro magnetoelastic actuator for robotics systems of nanotechnology. Proceedings of the 2018 IEEE Conference EIConRus pp. 1698-1701.
• Afonin SM (2018) Electro magnetoelastic nano- and micro actuators for mechatronic systems. Russian Engineering Research 38(12): 938-944.
• Afonin SM (2018) Structural-parametric model of electro elastic actuator for nanotechnology and biotechnology. Journal of Pharmacy and Pharmaceutics 5(1):8-12.
• Afonin SM (2018) Electro magnetoelastic Actuator for Nano mechanics. Global Journal of Research in Engineering: A Mechanical and Mechanics Engineering 18(2): 19-23.
• Bhushan B (2004) Springer Handbook of Nanotechnology. Springer, Berlin, New York p. 1222.

Abstract

A needle for obtaining a solid core (trephine) bone marrow biopsy sample from the posterior ilium is described. The needle is comprised of a hollow stainless-steel tube whose front-end diameter is reduced in comparison with the proximal segment. At its terminus the needle is also beveled and has six circumferentially spaced facets thereby forming a sharp cutting edge. The segment of the tube between the longer wider portion of the hollow tube and its smaller reduced diameter front end portion has a series of diamond shaped serrations/flutes on its surface which offer enhanced cutting ability as with a saw to assist in easy penetration of the needle through the dense cortical bone and into the marrow cavity.

Keywords: Single-use bone marrow biopsy needle; Core retention bone marrow biopsy needle; Bone marrow biopsy; Needle