Abstract

Through unbiased global optimization and density functional theory method, a series of stable icosahedral magnetic TMLi_{12 (TM=Sc-Fe) clusters are identified, where the 3d transition-metal element is embedded at the center of Li12 cage. Energy calculations and the moderate HOMO-LUMO gaps confirm their stability. Molecular orbitals analysis reveals the superatomic properties.}

Keywords: Superatoms; Stability; Magnetic Moment; Electronic Shell; Binding energy; Eb

Introduction

In recent years, the field of cluster science have been increasingly investigated [1-3]. Among them, superatoms, which can be used to mimic the chemical behaviour of atoms in the periodic table, are the ‘magic’ atomic clusters [4]. The valance electron of superatoms are accommodated in a series of quantized orbitals labeled as 1S, 1P, 1D, 2S, 1F, 2P, etc. Their stability can be understood by the jellium model, where the motions of electrons are assumed in a uniform positive spherical background composed by ionic charge of the cluster’s atomic nuclei and the innermost electrons [5,6]. The corresponding electronic levels in superatoms are 1S²1P⁶1D¹⁰2S²1F¹⁴2P⁶, etc., where 2, 8, 18, 20, 34 and 40, etc, are associated with magic clusters. Such superatoms are non-magnetic due to all the electrons paired. Khanna and coworkers proposed the concept of magnetic superatoms and took an isolated VCs₈ and a ligated protected MnAu₂₄(SH)₁₈ as examples in 2009, where the magnetic moments were acquired by the orbitals localized at the atomic sites and the stability was imparted by the diffuse states [7]. Since then, many reports about magnetic superatoms are emerged [8-12]. In this work, we use Li₁₃ as a prototype to design a new type superatom, which is formed by replacing the central atom of Li₁₃ with a 3d transition-metal element. Then, the stability and electronic properties of TMLi₁₂ are discussed.

Computational Methods

The structure of TMLi₁₂ (TM=Sc, Ti, V, Cr, Mn, Fe, Co and Ni) are located by unbiased global optimization method and density functional theory (DFT) of Gaussian16 package [13]. Frequency calculations prove that the icosahedron is a true energy minimum. The spin multiplicities (SMs) of each isomer are determined by comparison their energy of the same structure with different SMs, where the SM of the lowest energy structure is that of ground states. All the calculations are completed by adopting pure functional PW91 and SDD the basis set [14,15].

Results and Discussion

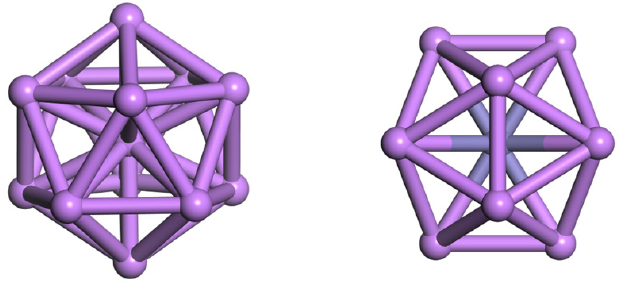
The geometric of pure Li13 cluster is a centred icosahedron with I_h symmetry as shown in Figure 1 and [16]. With the central lithium atom is substituted by 3d transition-metal elements (Sc, Ti, V, Cr, Mn, Fe, Co and Ni), and the structure retain still except CoLi₁₂ and NiLi₁₂ by unbiased global optimization method. To identify the stability of TMLi₁₂ (TM=Sc, Ti, V, Cr, Mn, and Fe), we examine

a) The average binding energy (Eb) per atom of the transition metal atom to the cluster,

b) The energy gaps of the highest occupied and lowest unoccupied molecular orbitals (HOMO-LUMO gaps).

Figure 1: Diagrams of pure Li₁₃ and TM@Li₁₂ (TM=Sc, Ti, V, Cr, Mn, and Fe) clusters with I_h symmetry.

The E_b is defined as the following equation:

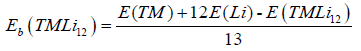
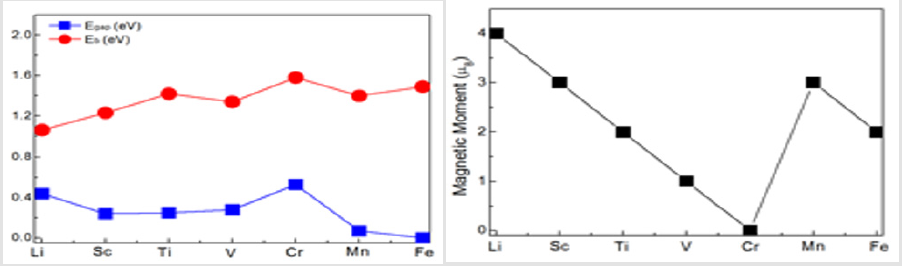
Where TM represents the 3d transition-metal atoms Sc, Ti, V, Cr, Mn, and Fe. E(TMLi₁₂) is the total energy of the I_h symmetry icosahedron. E(Li) and E(TM) are the total energy of the Li and TM atoms in the free state, respectively. From (Figure 2), it can be seen that the Eb of TMLi₁₂ (TM=Sc, Ti, V, Cr, Mn, Fe) clusters is higher than that of the corresponding pure Li₁₃. This indicate that embedding 3d transition-metal elements (Sc, Ti, V, Cr, Mn, and Fe) into Li₁₂ cage can enhance its stability. However, the results of energy gaps give small values, where large HOMO–LUMO gaps can enhance their stability and reduce their reactivity. Taking the gaps of typical magnetic superatoms as reference, the gaps are moderate, for example, V@ Na₈ (0.69 eV) [7] and MnSr₉ (0.35 eV) [8]. In addition, the gaps are underestimated by the standard GGA functionals, and an accurate gap need apply the hybrid functionals, for instance, the gap of FeLi₁₂ is 0.65 eV at the calculations of TPSSH/SDD. To examine the cause of their stability, we analyze the associated molecular orbitals, and take MnLi₁₂ as representative cluster, which has 19 effective valence electrons offered by lithium atom (2s^{1) and manganese atom (4s23d5), respectively. As shown in Figure 3, the lowest state over the whole cluster has 1S character. The next five states are 1D states while the degeneracy is broken into three groups of 1, 2 and 2 orbitals due to the oblate shape. The same occurs in the next 1P states, which is split into P_x, P_y, P_z and the degeneracy is completely removed. The next state is 2S, and the last occupied state has 2D character. Therefore, the electronic filling order of 19e MnLi₁₂ is 1S21D_α51P61D_β42S_α12D_α1, where the HOMO-LUMO gap (0.07 eV) is from the energy difference of 2D_α1 and 1D_β1. With three unpaired electrons, the total spin magnetic moment of MnLi₁₂ is 3.0 μB. Based on above discussion, the centred icosahedral MnLi₁₂ is a magnatic superatom, where its stability is acquired by having a spin magnetic moment of 3.0 μB. All the other clusters are magnatic superatoms except CrLi₁₂, which is a non-magnatic superatom due to all the electrons paired. The analysis is similar, and their magnetic moments also are display in Figure 2.}

Figure 2: Comparison of E_b and E_gap and the total magnetic moment of pure Li₁₃ and TMLi₁₂ (TM=Sc-Fe).

Figure 3: One electron energy levels and MOs of Mn@Li₁₂. Continuous lines represent the filled levels while the dotted lines is corresponding to the unfilled states.

Conclusion

In the work, we have demonstrated that cluster Li₁₂ endohedrally doped with a 3d transition-metal element (Sc, Ti, V, Cr, Mn, and Fe) can form stable clusters with I_h symmetry. These high symmetric clusters are identified as magnetic superatoms except CrLi₁₂, which is non-magnetic. Such a combination could be extended, where the transition-metal element in the same main element is embedded and superatoms also exist due to the same effective valence electrons.

Acknowledgement

This work is supported by the PhD Starting Fund of Guangdong Ocean University (120702/R17077).

References

• Claridge SA, Castleman Jr AW, Khanna SN, Murray CB, Sen A, et al. (2009) Cluster-assembled materials. ACSnano 3(2): 244-255.
• Castleman JAW, Khanna SN (2009) Clusters, superatoms, and building blocks of new materials. J Phys Chem C 117(7): 2664-2675.
• Ghosh A, Mohammed OF, Bakr OM (2018) Atomic-level doping of metal clusters. Acc Chem Res 51(12): 3094-3103.
• Knight WD, Clemenger K, de Heer WA, Saunders WA, Chou MY, et al. (1984) Electronic shell structure and abundances of sodium clusters. Phys Rev Lett 52(24): 2141-2143.
• Ekardt W (1984) Work function of small metal particles: Self-consistent spherical jellium-background model. Phys Rev B 29(4): 1558-1564.
• Ekardt W (1986) Theory of electronic excitations in coated metal particles: Jellium-on-jellium model. Phys Rev B 34(2): 526-533.
• Reveles JU, Clayborne PA, Reber AC, Khanna SN, Pradhan K, Sen P, Pederson MR (2009) Designer magnetic superatoms. Nat Chem 1: 310- 315.
• Medel V, Reveles JU, Khanna SN (2012) Magnetism of electrons in atoms and superatoms. J Appl Phys 112(6): 064313.
• Zhang M, Zhang J, Feng X, Zhang H, Zhao L, et al. (2013) Magnetic superatoms in VLin (n = 1-13) clusters: A first-principles prediction. J Phys Chem A 117(48): 13025-13036.
• Zhang X, Wang Y, Wang H, Lim A, Gantefoer G, et al. (2013) On the existence of designer magnetic superatoms. J Am Chem Soc 135(12): 4856-4861.
• Shibuta M, Ohta T, Nakaya M, Tsunoyama H, Eguchi T, et al. (2015) Chemical characterization of an alkali-like superatom consisting of a Taencapsulating Si₁₆ cage. J Am Chem Soc 137(44): 14015-14018.
• Bergeron DE, Castleman Jr. AW, Morisato T, Khanna SN (2004) Formation of Al₁₃I–: Evidence for the superhalogen character of Al13. Science 304(5667): 84-87.
• Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, et al. (2016) Gaussian 16, revision b.01; gaussian, inc.: Wallingford, ct.
• Hay PJ, Wadt WR (1985) Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J Chem Phys 82: 270-283.
• Perdew JP, Wang Y (1992) Accurate and simple analytic representation of the electron-gas correlation energy. Phys Rev B Condens Matter 45: 13244-13249.
• Fournier R, Bo Yi Cheng J, Wong A (2003) Theoretical study of the structure of lithium clusters. J Chem Phys 119: 9444-9454.

Abstract

Through unbiased global optimization and density functional theory method, a series of stable icosahedral magnetic TMLi_{12 (TM=Sc-Fe) clusters are identified, where the 3d transition-metal element is embedded at the center of Li12 cage. Energy calculations and the moderate HOMO-LUMO gaps confirm their stability. Molecular orbitals analysis reveals the superatomic properties.}

Keywords: Superatoms; Stability; Magnetic Moment; Electronic Shell; Binding energy; Eb