Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
Rostislav F Polishchuk*
Received: April 12, 2018; Published: April 27, 2018
*Corresponding author: Rostislav F Polishchuk, Astro Space Center of the Lebedev Physics Institute of Russian, Academy of SciencesLeninskii pr. 53, Moscow, 119991 Russia, Tel: 79164595680; Email: rpol@asc.rssi.ru
DOI: 10.26717/BJSTR.2018.04.001007
Local and non-local integral conservation laws in the Riemann-Cartan spaces are given. Hypothesis of the friedmons as dark matter particles is proposed. The mass of friedmon is near 109GeV and the symmetry group is dual for SU(2)one.
Keywords: Non-Local Integral Conservation Laws; Tetrad Currents; Planckian Density of the Original De Sitter World; Spin-Mass; Hypothesis of Friedmons as Dark Matter Particles
Gravitational field as some gauge field is a connection. The metric of the expanding Universe is near to de Sitter one. The Casmir operators in this case contain the combination of the spin and mass or spin-massas total parameter with physical significance due to the mixing of the spin-mass components by action of the de Sitter group SO(1,4) transformations [1].For example in the theory of super gravity with two complex Grassmanian values physical significance have eight real coordinates only (or four complex ones-with imaginary time and two space null coordinates) due to its mixing by the expanded Poincare group transformations. The Einstein equations connect masses with Riemannian curvature of space-time (events world for Minkowski). In frame of the Einstein- Cartan theory the spin-mass must be connected with the Riemann- Cartan space with the curvature and the torsion of the manifold of events [2-4].
There are 16 equations with the non-symmetric Einstein tensor gμv and the spin tensor Sμvλ as a result of the variation energy-momentum tensor with respect to the spinor connection 1-form. The Einstein equivalency principle (gravity and inertia are locally equivalent)is violated: the Cartan torsion is nontrivial for any observers. The Bianchi contracted identities give differential conservation laws for energy-momentum tensor. There is the nonlocal integral equivalent of its in General Relativity [5] (for example the integral on space contains also the integral on time). In the Riemann-Cartan space-time we deduce the follow formula( eaμdxμ-eigen 1-formsfor T(μv) with the eigen values pa, Kaμv - focusing tensors for 3-forms *ea,* is the Hodge operator):
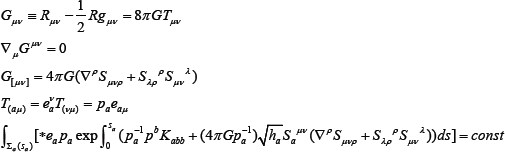
Here Σa(sa) are three equidistant cuts sa= const of the world ea-lines tube(of the matter for a=0) with the 3-volume 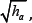 the signature of space-time is ( — + + + ), the mass density P° > 0 . But due to the spinre pulsing potential the effective density may be negative. The matte rcollapse will be succeeded due to the limit Planck an matter density and before it on the Cartanradius lcar [6] (below J is the spin of the particle with Compton length lcom, lpl is the Planck an length):
the signature of space-time is ( — + + + ), the mass density P° > 0 . But due to the spinre pulsing potential the effective density may be negative. The matte rcollapse will be succeeded due to the limit Planck an matter density and before it on the Cartanradius lcar [6] (below J is the spin of the particle with Compton length lcom, lpl is the Planck an length):
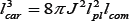
For example for proton 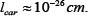 There is possible give also the local integral conservation low with aid the part δdea (the codifferential of the differential of the tetrad) in the Einstein tensor, contracted with the tetrad
There is possible give also the local integral conservation low with aid the part δdea (the codifferential of the differential of the tetrad) in the Einstein tensor, contracted with the tetrad 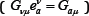 giving the tetrad current Sa [7]. There are the corresponding
giving the tetrad current Sa [7]. There are the corresponding
formulas with the Gibbons-Hawking Lagrangian[8]:
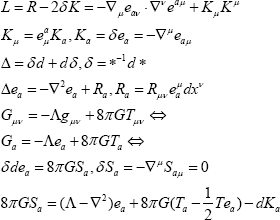
Now let us discuss the gravitational energy problem. These arch of the gravitational energy-momentum pseudo-tensor [9,10] was the mistake: its dependence on a choice of coordinates deprives it of the physical significance since - this significance has a frame of reference only as an additional invariant structure on the spacetime. It is impossible introduce the Diracequations in the Riemann- Cartanspace sand to solve the gravitational energy problem with out the lowering from the metric level to the tetradone. Even the accelerating frame of reference in the flat space-time permits us due to the Einstein equivalency principle to speak about nontrivial gravitation field (without the acceleration) with the gravitational energy -g2 /8πG (where g is the acceleration of the free full) and with the nontrivial Gibbons-Hawking Lagrangian. Einstein received the correct total energy of the island physical system due to using the asymptotically Cartesian frame of referent in the neighborhood of the space infinity [11]. Here the Cartesian coordinates are primary as equal to real translations. My teacher Abraham Leonidovich Zelmanov(1913-1887) has been searching unsuccessfully the chronometric invariant gravitational pseudotensor by the undetermined coefficients method. He introduced the monad vector field and the set of the integral time-like world lines as a frame of reference. Tetrad field includes the monad field, and the difference t0μ = S0μ - T0μ gives desired quantity.
There is interesting to note the Steven Weinbergpseudo- tensor[12]as the difference between energy-momentum tensor and the nonlinear parts of the Einstein tensor. But both the indices remained coordinate. Tetrad current is the analogical difference but our contracting of the energy-momentum tensor with the tetrad potential is an analog of the member AμJμ in frame of the electrodynamics. This approach we named as semitetradone: double contracted Einstein tensor with the tetrad gives 16 scalar equations instead one tensor equation in Einstein-Cartan theory. There are many different vacuums even in the flat space-time connecting by the Bogolyubov transformations. Vacuum plus matter is the whole physical system and conservation laws must be realized for vacuum plus matter only [13].
We propose introduce the gauge constraints for the vacuum background: that Г (connection module "gamma") be the sum of the product of the 12 complex Penrose spin coefficients [14] and complex conjugated ones. Condition Г = min gives primary frame of reference and corresponding physical vacuum. Vacuum is not in variant under the Lorentz transformations. Due to this noninvariance on tell about non-localization of the gravitational energy. We introduce the requirement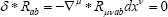 as the Riemann-canonicalgauge for gravitational theory. In this case we have then normal local integral conservation laws in gravity. We have the Bianchi identities and we introduce the six constraints on the canonical tetrad:
as the Riemann-canonicalgauge for gravitational theory. In this case we have then normal local integral conservation laws in gravity. We have the Bianchi identities and we introduce the six constraints on the canonical tetrad:
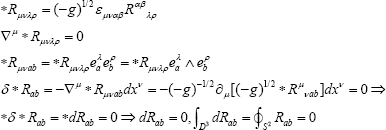
Now we have the six closed 2-forms Rab (dRab = 0) and local integral conservation laws for the canonical tetrad currents for the canonical tetrad field. The time-form e0 = dt implies S00 = 0, but for the Lorentz gauge we receive ordinary density for the weak gravitational radiation [10] and ordinary negative density of the gravitational energy in the static field. For the Hodge decomposition of tetrad into the sum of gradient, So closed and harmonic parts.
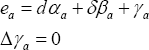
The second term gives nontrivial gravity and the last term - the gravitational radiation. The Gibbons-Hawking Lagrangian implies the density of the Hamiltonian as a partial divergence [11]. Integration in the de Sitter world (the set of the 3-spheres with empty cluster set) implies the trivial total mass-energy. There is important that Einstein tensor and energy-momentum tensor (directly proportional to the cosmological term) are non trivial and conserving. The Einstein-Cartane quations admit the next interpretation: the geometry of the space-time compensates the matter by the Riemannian curvature and the Cartan torsion. The string theory implies the string additions (that must be carried over right part of equations) that are important in origin of the Big Bang [15] (lowerl - the string length, α' - the inclination of the Regge trajectory):
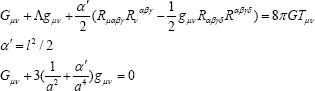
Here is string addition for the de-Sitter world. If the cosmological term ( Λ = 3/ a2 ) is absent,then it will be arise. The curvature radius must be changed with vacuum transformation when it gives it s mass to the mass-energy of the matter. The geometric empty is forbidden by the quantum mechanics, and any real physical vacuum implies the nontrivial geometry. The de Sitter world is the physical system with the conserving nontrivial scalar matter field. In conclusion we present the friedmons hypothesis as dark matter particles [16]. There is easy find the connection between the gravitational radius of the Sun rgr and the nucleon size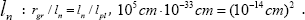 We propose that before the Big Bang the Universe was the 3-sphere (as the de Sitter world) with the limit Planckian density and respectively with the gravitational radius 10—13cm (the initial Lemaitre atom). Letus propose that this size is connected with the hypothetical particle friedmon( h /2π= c = 1 ):
We propose that before the Big Bang the Universe was the 3-sphere (as the de Sitter world) with the limit Planckian density and respectively with the gravitational radius 10—13cm (the initial Lemaitre atom). Letus propose that this size is connected with the hypothetical particle friedmon( h /2π= c = 1 ):
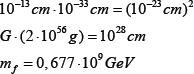
We propose that the symmetry group for the friedmon is the dual SU(2). In Standard model the particles with symmetry groups SU(3), U(1)are stable, but for the dual symmetry groups the particle with dual SU(2) group are stable only [17,18]. The interaction between the particles relating to the basic and the dual symmetry groups may be gravitational one only. The friedmons are heavy be- lepton formations with the quark type confinement. We propose that the Lemaitre atom after the transformation of the topological energetic modes into oscillation ones transmitted its mass to the ordinary substance. Even if the particle of dust gives its mass mto the de Sitter vacuum then we will receive the de Sitter world with the curvature radius a and the density ρ: 2π2a3ρ = m. For the Universe with its isotropy on the grand sizes its transformation into the scalar field (the de Sitter world) will be occur after the decay of the all elementary particles. May be there was the approximate equality of the total masses of the particles and dual particles with the hypothetical Grand Unification group as a product of the E8 on the dual one, containing the Standard model groups and dual groups as sub groups. The following evolution reduced to the predominance of the dark matter before the ordinary one. The future quantum gravity theory will give here the final answer.

